基本介紹
公式簡介
定義



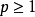
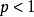
證明


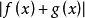
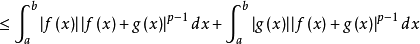






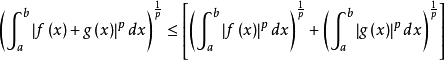
一般形式




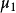

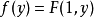

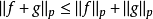
統計學形式
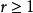



推廣定理


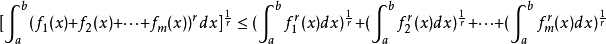

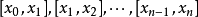






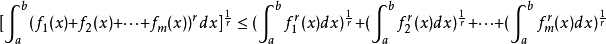



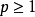
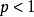


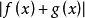
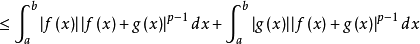






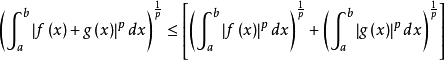




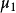

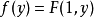

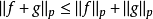
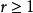





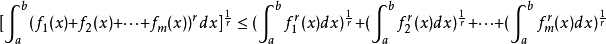

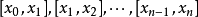






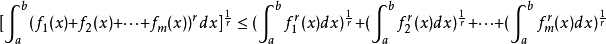
在數學中,閔可夫斯基不等式(Minkowski inequality)是德國數學家赫爾曼·閔可夫斯基提出的重要不等式,該不等式表明Lp空間是一個賦范向量空間。閔可夫斯基的主要工作在...
積分不等式是微積分學中的一類重要不等式,也為解決微分方程等方面的問題提供了 富有成效的理論工具。主要有楊不等式,施瓦茲不等式,閔可夫斯基不等式,延森不等式等...
閔可夫斯基(Hermann Minkowski,1864-1909)出生於俄國的 Alexotas (現在變成立陶宛的 Kaunas)。父親是一個成功的猶太商人,但是當時的俄國政府迫害猶太人,所以當閔...
在數學裡的泛函分析中,貝塞爾不等式是類似於勾股定理的一種不等式。貝塞爾不等式...bessel不等式相關條目 編輯 閔可夫斯基空間 柯西不等式 三角不等式 完備空間...
同時介紹了幾個常見的著名不等式,如排序不等式、赫爾德不等式、契比雪夫不等式和閔可夫斯基不等式,內容豐富、全面。重點介紹了平均值不等式與柯西不等式在證明不等式...
柯西不等式是由大數學家柯西(Cauchy)在研究數學分析中的“流數”問題時得到的。但從歷史的角度講,該不等式應當稱為Cauchy-Buniakowsky-Schwarz不等式【柯西-布尼亞...
在數學領域, 馬勒不等式陳述說由兩個無窮正項序列的對應項的和構成序列的幾何...馬勒不等式參閱 編輯 閔可夫斯基不等式 參考資料 1. M.I. Voitsekhovskii ...
幾何數論又稱數的幾何,套用幾何方法研究某些數論問題的一個數論分支。在數論中,幾何數論研究凸體和在n維空間整數點向量問題。幾何數論於1910由赫爾曼·閔可夫斯基創立...
利用赫爾德不等式容易得到閔可夫斯基不等式:定理4 設 是兩列實數,則有閔可夫斯基不等式當數列 對應成非負比例時等號成立。定義設 互為共軛指數,根據赫爾德不等式,...
從不等式:|f+g|≤ 2(|f|+ |g|)可知,兩個p次可積函式的和,也是一個p次可積函式。另外,容易證明;閔可夫斯基不等式的積分形式說明三角不等式對成立。滿足...
可以驗證p-範數確實滿足範數的定義。其中三角不等式的證明不是平凡的,這個結論通常稱為閔可夫斯基(Minkowski)不等式。當p取 的時候分別是以下幾種最簡單的情形:1-...
7.1.2 赫爾德不等式7.1.3 閔可夫斯基不等式7.2 向量範數7.2.1 向量範數7.2.2 向量範數的等價性7.3 矩陣範數7.3.1 矩陣範數...
赫爾德不等式可以證明 空間上一般化的三角不等式,閔可夫斯基不等式,和證明 空間是 空間的對偶[1] 。赫爾德條件備註 編輯 在赫爾德共軛的定義中,1/∞意味著零。...
從不等式:|f+g|≤ 2(|f|+ |g|)可知,兩個p次可積函式的和,也是一個p次可積函式。另外,容易證明 ;閔可夫斯基不等式的積分形式說明三角不等式對 成立。...
;閔可夫斯基不等式的積分形式說明三角不等式對 成立。滿足這樣條件的 構成一個半範數,令 成為一個半賦范向量空間。之所以是半範數,是因為滿足 的函式f不一定是零...
