數學上,若兩個實數p,q>1,且1/p+1/q=1 ,稱p,q為共軛指數(conjugate indices),一般定義q=∞為p=1的共軛指數。
基本介紹
- 中文名:共軛指數
- 外文名:conjugate indices
- 所屬學科:數學
- 套用:赫爾德不等式、對偶空間等
定義,相關套用及定理,
定義
若 ,且
,且 ,稱
,稱 互為共軛指數。
互為共軛指數。



相關套用及定理
引理1設 是一對共軛指數,則對任何正數A,B,有
是一對共軛指數,則對任何正數A,B,有







指數 時的赫爾德不等式
時的赫爾德不等式


定理3 設 是一組共軛指數,即
是一組共軛指數,即 ,設
,設 是
是 列實數(列長可以是有限數n,也可以是無窮),則有多重赫爾德不等式
列實數(列長可以是有限數n,也可以是無窮),則有多重赫爾德不等式




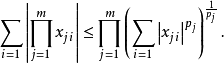

利用赫爾德不等式容易得到閔可夫斯基不等式:
定理4 設 是兩列實數,則有閔可夫斯基不等式
是兩列實數,則有閔可夫斯基不等式

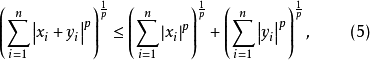

定義 設 互為共軛指數,根據赫爾德不等式,對於每個
互為共軛指數,根據赫爾德不等式,對於每個 ,則
,則



定理5設 互為共軛指數,若
互為共軛指數,若 ,則
,則





定理6設 是
是 的開集,
的開集, 互為共軛指數,若
互為共軛指數,若 ,則對
,則對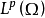 中的任一線性泛函G(即
中的任一線性泛函G(即 ),一定存在唯一的函式
),一定存在唯一的函式 ,使得
,使得 ,且對任意
,且對任意 ,下式成立:
,下式成立: