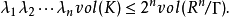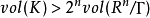基本介紹
簡介,歷史,近現代研究,重要結論,影響,
簡介
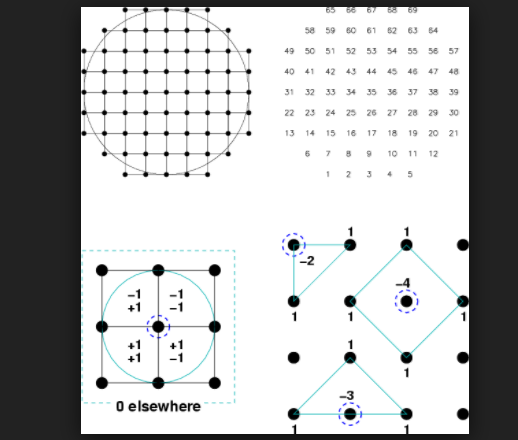
幾何數論是由德國數學家、物理學家閔可夫斯基等人開創和奠基的。主要在於透過幾何觀點研究整數(在此即格點)的分布情形。幾何數論研究的基本對象是“空間格網”。在給定的直角坐標系上,坐標全是整數的點,叫做整點;全部整點構成的組就叫做空間格網。空間格網對幾何學和結晶學有著重大的意義。最著名的定理為閔可夫斯基不等式(Minkowski 定理)。由於幾何數論涉及的問題比較複雜,必須具有相當的數學基礎才可以深入研究。
歷史
1891年,閔科夫斯基發表了關於幾何數論的第一篇論文,並於1896年出版了《數的幾何學》一書。從此,數的幾何成為數論的一個獨立分支。
近現代研究
在1930年至1960年的很多數論學家取得了很多成果(包括路易·莫德爾,哈羅德·達文波特和卡爾·路德維希·西格爾)。近年來,Lenstra,奧比昂,巴爾維諾克對組合理論的擴展對一些凸體的格數量進行了列舉。
施密特子空間定理;
在幾何數論的子空間定理,由沃爾夫岡·施密特在1972年證明;
重要結論
閔可夫斯基定理,有時也被稱為閔可夫斯基第一定理:
則λK在Γ中ķ線性無關,則有: