基本介紹
- 中文名:無理數
- 外文名:Irrational number
- 別稱:無限不循環小數
- 提出者:希伯索斯
- 套用學科:數學
- 性質:不能用分數進行表示
- 對應概念:有理數
- 所屬範圍:實數
定義

歷史

 分數=有限小數+無限循環小數,無限不循環小數是無理數
分數=有限小數+無限循環小數,無限不循環小數是無理數證明方法




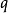

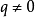










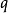
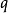

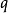

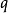


拓展











實例


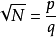



















 分數=有限小數+無限循環小數,無限不循環小數是無理數
分數=有限小數+無限循環小數,無限不循環小數是無理數



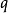

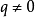










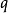
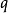

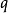

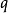















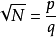
















無理數,也稱為無限不循環小數,不能寫作兩整數之比。若將它寫成小數形式,小數點之後的數字有無限多個,並且不會循環。 常見的無理數有非完全平方數的平方根、π...
無理數e編輯 鎖定 討論999 e在數學中是代表一個數的符號,其實還不限於數學領域。在大自然中,建構,呈現的形狀,利率或者雙曲線面積及微積分教科書、伯努利家族等...
連續性與無理數(Stetigkeit and irrationaleZahlen)西方現代數學著作,德國數學家戴德金(Dedekind, (J. W. )R.)著,發表於1872年...
如果代數式中含有表達式的開方運算,而表達式中又含有字母,則此代數式就叫做這些字母的無理代數式,簡稱無理式(irrational expression)。無理式與無理數(irrational ...
《無理數的極限》是連載的一部網路小說,作者是空心米。...... 《無理數的極限》是連載的一部網路小說,作者是空心米。中文名 無理數的極限 作者 空心米 小...
有理數是“數與代數”領域中的重要內容之一,在現實生活中有廣泛的套用,是繼續學習實數、代數式、方程、不等式、直角坐標系、函式、統計等數學內容以及相關學科知識...
《多項式和無理數》是2008年哈爾濱工業大學出版社出版的圖書,作者是馮貝葉。...... 《多項式和無理數》是2008年哈爾濱工業大學出版社出版的圖書,作者是馮貝葉。...
《數學·統計學系列·多項式和無理數》從數的起源講起,逐步介紹數的發展和新的各種性質及其套用,其中也包括了數學分析、實變函式和高等代數的一些入門知識,最後...
第一次數學危機,是數學史上的一次重要事件,發生於大約公元前400年左右的古希臘時期,自根號二的發現起,到公元前370年左右,以無理數的定義出現為結束標誌。這次...
(Hippasu,米太旁登地方人,公元前5世紀)發現了一個腰為1的等腰直角三角形的斜邊(即根號2)永遠無法用最簡整數比(不可公度比)來表示,從而發現了第一個無理數...
實數,是有理數和無理數的總稱。數學上,實數定義為與數軸上的實數,點相對應的數。實數可以直觀地看作有限小數與無限小數,實數和數軸上的點一一對應。但僅僅以...
分母有理化(fēn mǔ yǒu lǐ huà)(Rationalize the denominator),又稱"有理化分母",指的是在二次根式中分母原為無理數,而將該分母化為有理數的過程,也...
實數指數冪基本包括整數指數冪、分數指數冪與無理數指數冪。其一般形式為 a^n (n是實數)...
π是個無理數,即不可表達成兩個整數之比,是由瑞士科學家約翰·海因里希·蘭伯特於1761年證明的。 1882年,林德曼(Ferdinand von Lindemann)更證明了π是超越數,即...
3 用途 4 數學 5 函式 6 利潤 7 歷史發展 ▪ 實驗時期 ▪ 幾何法時期 ▪ 分析法時期 ▪ 計算機時代 8 證明為無理數 9 希臘字母 Π...
要追溯虛數出現的軌跡,就要聯繫與它相對實數的出現過程。我們知道,實數是與虛數相對應的,它包括有理數和無理數,也就是說它是實實在在存在的數。...
數學危機是數學在發展中種種矛盾, 數學中有大大小小的許多矛盾,比如正與負、加法與減法、微分與積分、有理數與無理數、實數與虛數等等。但是整個數學發展過程中...
畢達哥拉斯的學生希伯索斯第一次發現邊長為1的正方形的對角線並不能用整數比來表達,出現了無理數。畢達哥拉斯學派一開始不認同無理數的存在。由於希伯索斯堅持...
在希帕索斯悖論發現之前,人們僅認識到自然數和有理數,有理數理論成為占統治地位的數學規範,希帕索斯發現的無理數,暴露了原有數學規範的局限性。由此看來,希...
