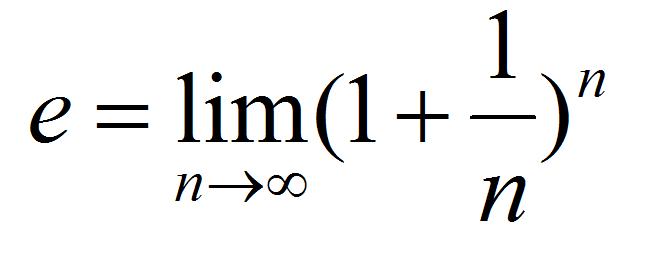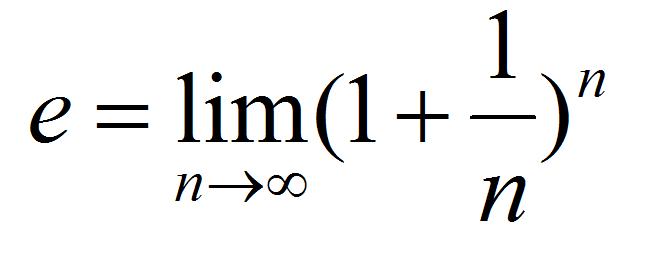基本介紹
- 中文名：無理數e
- 類型：數的符號
- 不限於：數學領域
- 小數點：後面兩千位
e的定義,e的範圍,e的故事,引入,對數,利息,e的套用,數學名人,對數表的發明者,對數受到的讚譽,微積分教科書,伯努利家族,e的大小,e小數點後面幾位,e的極限表示,
e的定義
當n→∞時，(1+1/n)^n的極限
註：x^y表示x的y次方。
e的範圍
隨著n的增大，底數越來越接近1，而指數趨向無窮大，那結果到底是趨向於1還是無窮大呢？其實，是趨向於2.71828……，不信你用計算器計算一下，分別取n=1,10,100,1000。但是由於一般計算器只能顯示10位左右的數字，所以再多就看不出來了。
e的故事
引入
這裡的e是一個數的代表符號，而我們要說的，便是e的故事。這倒叫人有點好奇了，要能說成一本書，這個數應該大有來頭才是，至少應該很有名吧？但是打開我們的記憶搜尋器，大部分人能想到的重要數字，除了0和1外，大概就只有和圓有關的π了，了不起的話，再加上虛數單位的i=√-1。那么這個e究竟是何方神聖呢？
對數
在高中數學裡，大家都學到過對數（logarithm）的觀念，也用過對數表。教科書里的對數表，是以10為底的，叫做常用對數（common logarithm）。課本里還簡略提到，有一種以無理數e=2.71828……為底數的對數，稱為自然對數（natural logarithm），這個e，正是我們故事的主角。不知這樣子說，是否引起你更大的疑惑呢？在十進位制系統里，用這樣奇怪的數為底，難道會比以10為底更「自然」嗎？更令人好奇的是，長得這么奇怪的數，會有什麼故事可說呢？
利息
這就要從以前說起了。至少在微積分發明之前半個世紀，就有人提到這個數，所以雖然它在微積分里常常出現，卻不是隨著微積分誕生的。那么是在怎樣的狀況下導致它出現的呢？一個很可能的解釋是，這個數和計算利息有關。
我們都知道複利計息是怎么回事，就是利息也可以並進本金再生利息。但是本利和的多寡，要看計息周期而定，以年周期來算的話，可以一年只計息一次，也可以每半年計息一次，或者一季一次，一月一次，甚至一天一次；當然計息周期愈短，本利和就會愈高。有人因此而好奇，如果計息周期無限制地縮短，比如說每分鐘計息一次，甚至每秒，或者每一瞬間（理論上來說），會發生什麼狀況？本利和會無限制地加大嗎？答案是不會，它的值會穩定下來，趨近於一極限值，而e這個數就現身在該極限值當中,所以e可以定義成一個極限值，但是在那時候，根本還沒有極限的觀念，因此e的值應該是觀察出來的，而不是用嚴謹的證明得到的。
e的套用
這個與計算複利關係密切的數，和數學領域不同分支中的許多問題都有關聯。在討論e的源起時，除了複利計算以外，事實上還有許多其他的可能。問題雖然都不一樣，答案卻都殊途同歸地指向e這個數。比如其中一個有名的問題，就是求雙曲線y=1/x底下的面積。雙曲線和計算複利會有什麼關係，不管橫看、豎看、坐著想、躺著想，都想不出一個所以然對不對？可是這個面積算出來，卻和e有很密切的關聯。我才舉了一個例子而已，這本書里提到得更多。e的影響力其實還不限於數學領域。大自然中太陽花的種子排列、鸚鵡螺殼上的花紋都呈現螺線的形狀，而螺線的方程式，是要用e來定義的。建構音階也要用到e，而如果把一條鏈子兩端固定，松松垂下，它呈現的形狀若用數學式子表示的話，也需要用到e。
數學名人
對數表的發明者
世界上第一個對數表是納皮爾（John Napier）發明的。納皮爾在十六世紀末、十七世紀初利用紙筆一項一項慢慢地算，而又還不能利用對數來化乘除為加減，好簡化計算。因此納皮爾整整花了二十年的時間建立他的對數表。
對數受到的讚譽
對數發明後，受到了熱切的歡迎，許多歐洲甚至中國的科學家都迅速採用，連納皮爾也得到了來自世界各地的讚譽。最早使用對數的人當中，包括了大名鼎鼎的天文學家克卜勒 ，他利用對數，簡化了行星軌道的繁複計算。
微積分教科書
在《毛起來說e》中，還有許多我們在一般數學課本里讀不到的有趣事實。比如第一本微積分教科書是誰寫的呢？（假如你曾受微積分課程之苦，也會想知道誰是「始作俑者」吧？」）是羅必達先生。對啦，就是羅必達法則（L'Hopital's Rule）的那位羅必達。但是羅必達法則反倒是約翰．伯努利先發現的。不過這無關乎剽竊的問題，他們之間是有協定的。
伯努利家族
說到伯努利可就有故事說了，這個家族實在不得了，別的家族出一位天才就可以偷笑了，而他們家族的天才是用「量產」形容。伯努利們前前後後在數學領域中活躍了一百年，他們的諸多成就（不僅止於數學領域），就算隨便列一列，也有一本書這么厚。不過這個家族另外擅長的一件事就不太敢恭維了，那就是吵架。自家人吵不夠，也跟外面的人吵（可以說是「表里如一」）。連爸爸與兒子合得一個大獎，爸爸還非常不滿意，覺得應該由自己獨得，居然氣得把兒子趕出家門；和現代的許多「孝子」們比起來，這位爸爸真該感到慚愧。
e的大小
e小數點後面幾位
e=2.718281828459045235360287471352662497757247093699959574966967627724076630353 5475945713821785251664274274663919320
e的極限表示
e=lim<x-->0>(1+1/x)^x
=lim<n-->+∞>{1,2,3,4,…，n}
=lim<x-->+∞>∑(0,x)1/i!
註：{1,2,3,4,…,n}=1+1/{1+1/[2+(1/3+{1/4+…+(1/n)]})]…}
