最概然值(most probable value)亦稱“最或然值”。按機率最大的最優估計原理求得的參數估值。在測量中處理帶有偶然誤差的觀測值時,參數的最概然值就是按最小二乘法原理求得的估值。
基本介紹
定義,舉例,最概然速率,套用,
定義
設有 個變數:
個變數: ,若
,若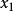 有
有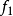 個,
個, 有
有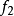 個,...,
個,..., 有
有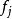 個。可以畫出其對應的階梯圖。每個階梯的中央值叫做“階梯值”,是該階梯的代表值。
個。可以畫出其對應的階梯圖。每個階梯的中央值叫做“階梯值”,是該階梯的代表值。


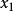
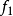

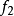

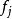
從階梯值小的階梯開始,排列階梯值。中心位置的階梯值叫做“中央值”或“中位值”。
具有代表性的是最大密度的階梯。該值稱為“最概然值”或“模”。也有人稱之為“眾數”。
舉例
某班的身高情況如圖1所示:
則在本例中不難得到,144-147的階梯值是145.5;中央值是157.5;最概然值是160.5。 圖1某班學生身高情況
圖1某班學生身高情況
 圖1某班學生身高情況
圖1某班學生身高情況最概然速率
平衡態時,氣體分子熱運動的速率分布服從麥克斯韋速率分布律,與速率分布函式的極大值對應的速率,曾稱最可幾速率,記作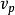 。將速率分成相等的速率間隔,不同間隔內的分子數占總分子數的百分比不同,而包含著vp的速率間隔內的分子數占總分子數的百分比最大,或者說對一個分子來說,其速率取各間隔內速率值的機率大小不一樣,而取包含著
。將速率分成相等的速率間隔,不同間隔內的分子數占總分子數的百分比不同,而包含著vp的速率間隔內的分子數占總分子數的百分比最大,或者說對一個分子來說,其速率取各間隔內速率值的機率大小不一樣,而取包含著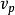 那個間隔內速率值的機率最大,因此稱為最概然速率。
那個間隔內速率值的機率最大,因此稱為最概然速率。
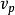
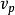
套用
最小二乘法是KArl Friedrich Gauss在1795年研究行星軌跡預報時提出的,是一種處理大量觀測數據行之有效的數學方法,也是科技工作者最熟悉的套用數學工具之一。
最小二乘法認為根據實驗獲得的數據來求導我們希望的未知參數時,最恰當的值就是最概然值(最可能的值)。最概然值應能保證實際觀測值和計算值之間差的平方和達到最小。
