星形集

星形集(star set)是一類比凸集更廣泛的子集。設E是d維實仿射空間X中的一個子集。x∈E，若對任意的y∈E，有[x，y]E，則稱E是一個在x處的星形集。

凸集是一類特殊的點集。若對於點集M中任意兩點A和B，線段AB上的每一點都屬於點集M，則M就叫做凸集。

基本介紹

• 中文名：星形集
• 外文名：star set
• 領域：數學
• 學科：集合
• 性質：比凸集更廣泛的子集
• 空間：d維實仿射空間

概念

星形集(star set)是一類比凸集更廣泛的子集。設E是d維實仿射空間X中的一個子集。x∈E，若對任意的y∈E，有[x，y]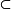E，則稱E是一個在x處的星形集。一個凸集在其每一點處都是星形集。星形集是連通的，並且是弧連通的。設A是d維歐幾里得空間X中的一個緊集，並且對於任意的：

存在y∈X，使得[x_i，y]A對於任意的i=1，2，…，d+1成立，則A是一個星形集。

集合

集合是現代數學的一個重要的基本概念。當我們把一組確定的事物作為整體來考察時，這一整體就叫做集合。

例如，(1)從1到10這10個自然數的全體；(2)小於100的所有質數的全體；(3)全體自然數；(4)一個班所有學生這一整體；(5)世界上所有國家組成的一個整體；等等，它們都是集合的例子。

上述例子可以看出，它們都是分別由不同的對象組成的一個整體，它們的特點是有確定的對象和具有一定的範圍。所以集合這個概念可以用以下的語言來描述：

集合是具有一定範圍的、確定的對象的全體。集合也簡稱為集。

在數學中，集合是一個不加定義的“原始概念”。這就是說，不能用比它更原始的概念去定義它。因此，集合在數學中被作為原始的最基本的概念來定義其它數學概念。集合是數學概念的出發點。

集合概念具有以下一些屬性：

(1)集合指的是一類事物的整體，而不是指其中的個別事物。

(2)集合中的任一對象具有確定性，即對於任何事物，可以通過某種法則確定其是否屬於某集合，或不屬於某集合，二者必居其一。(應指出，不具有這條屬性的，界限不清的集合是模糊集合。我們這裡所說的集合不是模糊集合，而是普通集合。)

(3)在一般情況下，約定一個集合中的各個對象是互不相同的。凡一個集合中所有相同的對象均應合併起來成為一個對象。例如，由1，1，2，2四個數組成的集合，應變成由1，2兩個數組成的集合。

(4)在一般情況下，集合只與組成它的成員有關，而與它的成員的順序無關。如由1，2，3，4組成的集合與由2，1，4，3組成的集合是同一個集合。

(5)一個集合不必由同一類事物作為它的對象。例如，由2， 3，a，b可以組成一個集合。

集合一般用大寫字母A，B，C，…表示。

子集

子集是表示一個集合與另一個集合的一種關係。

設A和B是兩個集合，若集合B包含A，或集合A包含於B，即A⊆B或B⊇A，則把集合A叫做集合B的子集，並把集合B叫做集合A的擴張集(或母集)，簡稱擴集。

例如，集合A={1，2}是集合B={1，2，3，4，5}的子集；再如，設集合A={a|a為直角三角形}，集合B={a|a為三角形}，則A就是B的子集，B是A的擴集。

根據子集的定義和包含關係的性質，有：

①任何一個集合都是它自身的子集，同時也是它自身的擴集；

②空集Φ是一切集合的子集；

③設A，B，C是三個集合，若A是B的子集，B又是C的子集，則A也一定是C的子集。

若一個集合A是集合B的且異於B的子集，則稱A是B的真子集，B叫做A的真擴集，記作A⊂B或B⊃A。

根據真子集的定義，有：

①若集合A是集合B的真子集，則A的每一個元素都屬於B，但B中至少有一個元素不屬於A；

②空集Φ是任何非空集合的真子集，任何非空集合都是空集Φ的真擴集；

③任何一個集合A都不是它自身的真子集。

凸集

一類特殊的點集。若對於點集M中任意兩點A和B，線段AB上的每一點都屬於點集M，則M就叫做凸集。

根據凸集的定義可知，平面、半平面(包括開半平面和閉半平面)、帶形區域、直線、射線和線段等都是凸集。

還可以證明，凸多邊形區域、圓域、橢圓域等都是凸集。

另外約定，空集Φ和只含一個點的點集都是凸集。

若M₁，M₂是任意兩個凸集，則它們的交集M=M₁∩M₂也是凸集。這個結論也可以推廣到任意多個凸集的情況，即若M₁，M₂，…，M_n是任意n個凸集，則它們的交集也是凸集。

M=M₁∩M₂∩…∩M_n

凸集的概念主要用於覆蓋問題。例如，當兩個點集M，N的點之間可以建立起一一對應，並且對於點集M中的任意兩點A，B和點集N中對應的兩點A′B′，有AB/A′B′=k(k為正常數)時，就稱點集M與N為相似點集。若點集M與N相似，M的直徑大於N的直徑，並且M是凸集，則點集M能覆蓋點集N。

仿射空間

仿射空間是數學中的幾何結構，這種結構是歐式空間的仿射特性的推廣。在仿射空間中，點與點之間做差可以得到向量，點與向量做加法將得到另一個點，但是點與點之間不可以做加法。

從基本數學概念上來說，一個坐標系對應了一個仿射空間 (Affine Space)，當矢量從一個坐標系變換到另一個坐標系時要進行線性變換(Linear Transformation)。對點來說， 要進行仿射變換(Affine Transformation)。這就是我們利用同源坐標的理由。它能在對矢量進行線性變換的同時對點進行仿射變換。坐標變換的基本操作就是將變換矩陣乘以矢量或點。

仿射空間是沒有起點只有方向與大小的向量所構成的向量空間。假設有甲乙兩人，其中甲知道一個空間中真正的原點，但是乙認為另一個點p才是原點。現求兩個向量a和b的和。乙畫出 p到a和 p 到b 的箭頭， 然後用平行四邊形找到他認為的向量 a + b。但是甲認為乙畫出的是向量p+(a − p) + (b − p)。同樣的，甲和乙可以計算向量a和b的線性組合，通常情況下他們會得到不同的結果。

然而，請注意：如果線性組合係數的和為1，那么甲和乙將得到同樣的結果！仿射空間就是這樣產生的：甲知道空間的"線性結構"。但是甲和乙都知道空間的"仿射結構"，即他們都知道空間中仿射組合的值，其中仿射組合的定義為係數和為1的線性組合。

具有仿射結構的集合就是一個仿射空間。

歐幾里得空間

簡稱歐氏空間。既是幾何學的研究對象，又是代數學的研究對象。在幾何學中，歐氏空間是滿足全部歐幾里得公理的幾何空間。它的幾何是研究幾何圖形的度量性質和度量不變數的歐幾里得幾何(簡稱歐氏幾何)，包括普通平面幾何和立體幾何的全部理論。

歐氏幾何空間按維數的不同而有一維歐氏空間(即歐氏直線)、二維歐氏空間(即歐氏平面)和三維歐氏空間(即普通空間，在幾何學中也常簡稱歐氏空間)。在代數學中，歐氏空間是實數域上的一個線性空間，在其中規定了一個稱為內積的二元實函式。歐氏線性空間的維數可以是任意的自然數。容易在同維數的歐氏幾何空間與歐氏線性空間之間建立直接的聯繫。在歐氏幾何空間中取定一點作為公共的起點，空間每一點就決定一個以該點作為終點的向量。這種向量的全體構成的集合在向量加法和數乘向量的乘法下就是一個線性空間。再以通常向量的數量積作為線性空間中向量的內積，這個線性空間就是一個歐氏線性空間。反之，線上性空間取定基底後，n維線性空間中的向量可以用n元數組作為坐標表示，再把n維歐氏線性空間的向量的坐標看做n維歐氏幾何空間中建立了直角坐標系後點的坐標，這樣就在n維歐氏線性空間的向量和n維歐氏幾何空間的點之間建立了一一對應，並且當取後者的坐標原點作為公共的起點，由後者的每個點作為終點所決定的向量，其坐標正好與前者的對應向量的坐標相同，由其數量積所確定的歐氏線性空間，也與前者完全合一。

總之，按照以上的討論，在同維數的幾何空間和歐氏線性空間之間可以建立一一對應，並在此對應下保持著各自的幾何、代數結構。這也是將後來發展的代數體系與先發展的幾何體系取同一名稱——歐幾里得空間的原因。