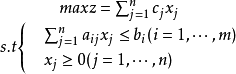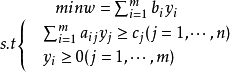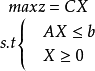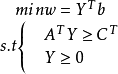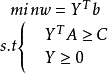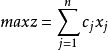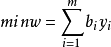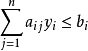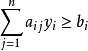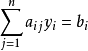對偶規劃(dual programming)一類線性規劃問題，指由原線性規劃問題按如下對稱規律構成的新線性規劃問題：若原問題(P)為maxz=CTX，滿足{AX≤b，x≤0 }，則對稱的新問題(D)為minw=yTb，滿足{yTA≥c，y≥0 }，這裡y為m維列向量，新問題(D)稱為原線性規劃的對偶規劃。
基本介紹
- 中文名：對偶規劃
- 外文名：Dual programming
- 性質：線性規劃問題
- 提出者：馮·諾伊曼
- 提出時間：1947年
- 學科：數學
發現簡史,定律定義,標準形式,矩陣形式,對偶問題轉化,一般形式,非對稱形式,性質,對稱性,弱對偶性,最優性,對偶性,互補鬆弛性,
發現簡史
對偶規劃最初是由馮·諾伊曼（vonNeu-mann，J.）於1947年提出來的，以後庫恩（Kuhn，H.W.）和塔克爾(Tucker，A.W.）證明了對偶定理。哥德曼(Goldman，A.J.）和塔克爾於1956年比較系統地敘述了對偶規劃的理論。
對偶線性規劃的經濟背景是：若原問題是利用有限資源安排最優生產方案，以獲得最大總產值的線性規劃問題，則它的對偶問題就是在相同資源的條件下，正確估計資源的使用價值，以達到支付最少費用的線性規劃問題。簡言之，若原問題為求解資源的最優配置問題，則對偶問題就是求解估價資源的使用價值問題。
定律定義
標準形式
假定原問題是最大化問題，即線性規劃問題（LP），它的標準形式：
其對偶問題（DLP）如下式所示：
矩陣形式
用矩陣形式表示，對稱形式的線性規劃問題的原問題為：
其對偶問題為：
或寫作
對偶問題轉化
一般形式
上述都是一對對稱形式的對偶線性規劃，在原線性規劃問題與對偶線性規劃問題之間有著整齊的對稱性，其特徵是：
1.一個問題求極大max，對應另一個問題求極小min。
2.求極大問題中的約束條件為“≤”，求極小問題中的約束條件為“≥”。
3.原問題中有個變數，對偶問題中就有個約束條件。原問題中有m個約束條件，對偶問題中就有m個變數（稱為對偶變數）。
4.原問題的目標函式中變數的係數就是對偶問題約束條件的常數項。原問題中約束條件的常數項就是對偶問題目標函式中變數的係數。
6.原問題與對偶問題中的變數均有非負約束。
非對稱形式
因為並非所有線性規劃問題具有對稱形式，故對下面討論更加一般形式下線性規劃問題如何寫出其對偶問題。無論是堆成或非堆成的線性規劃問題在寫出其對偶問題時，對於A、B、C和目標函式的對應關係都適用，區別的只是約束條件的形式與其對應變數的取值。下面將對稱或不對稱線性規劃原問題同對偶問題的轉換時的對應關係，統一歸納為下表所示形式。
項目 | 原問題(對偶問題) | 對偶問題(原問題） |
A | 約束係數矩陣 | 約束係數矩陣的轉置 |
B | 約束條件右端項向量 | 目標函式中的價格係數向量 |
C | 目標函式中的價格係數向量 | 約束條件右端項向量 |
目標函式 |  |  |
n個變數xj（j=1,···,n) | n個約束條件（j=1,···,n) | |
xj≥0 |  | |
xj≤0 | | |
xj無約束 | | |
n個約束條件（i=1,···,=m) | m個變數yi（i=1,···,m) | |
 | yi≥0 | |
 | yi≤0 | |
 | yi無約束 | |
