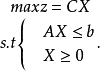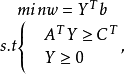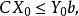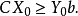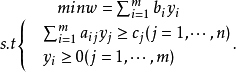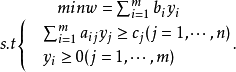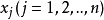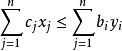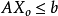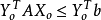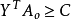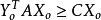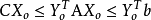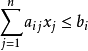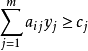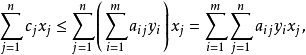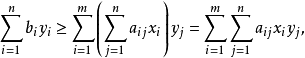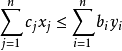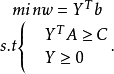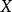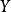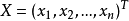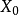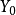弱對偶性

弱對偶性（weak duality）是運籌學中的術語，指的是在極大化線性規劃問題中，如果X是原問題的任意可行解，Y是對偶問題的任意可行解，那么有CX≤Yb。

基本介紹

• 中文名：弱對偶性
• 外文名：weak duality
• 範疇：運籌學
• 套用：線性規劃問題

定義

矩陣形式

用矩陣形式表示，對稱形式的線性規劃問題的原問題為：

其對偶問題為：

或表示為：

其中， 和 均是列向量， ， ，上標 表示轉置。

若 是原問題的可行解， 其對偶問題的可行解，則恆有：

如果原問題是求極小化問題上述結論的符號相反：

標準形式

假定原問題是最大化問題即線性規劃問題（LP）的標準形式：

其對偶問題（DLP）如下式所示：

若 是原問題的可行解，y_i=(j=1,2,···,m)是其對偶問題的可行解，則恆有：

定律推論

以下是根據弱對偶性的推論：

1. 原問題是極大化問題時，原問題任意可行的目標函式值是其對偶問題目標函式值的下界；反之對偶問題任一可行解的目標函式值是其原問題目標函式的上界。
   
2. 原問題是極小化問題時，原問題任意可行的目標函式值是其對偶問題目標函式值的上界；反之對偶問題任一可行解的目標函式值是其原問題目標函式的下界。
   
3. 如果原問題（有可行解且）目標函式值無界即有無界解，則其對偶問題無可行解；反之對偶問題(有可行解且)目標函式值無界，則其原問題無可行解。（可行解無界，就不能存在為其上下界的可行解。）
   
4. 性質2的逆命題不成立，因為：當對偶問題無可行解時，其原問題或具有無界解或無可行解，反之亦然。
   
5. 若原問題有可行解而對偶問題無可行解，則原問題目標函式無界；反之對偶問題有可行解而其對偶問題無可行解，對偶問題的目標函式無界。
   

推導過程

矩陣形式

由於原問題的任一可行解X_o必定滿足約束條件： ，在不等式兩邊同時右乘對偶問題可行解Y_o，有 ；且對偶問題的任一可行解Y_o必定滿足約束條件： ，在不等式兩邊同時左乘原問題可行解X_o，有 ，可以推導出它們的目標函式值有以下關係：

（原問題的目標函式值） （對偶問題的目標函式值)

標準形式

由於原問題的任一可行解滿足 ，對偶問題的任一可行解滿足

證：因為

所以，