可檢性

如果存在一個觀測器增益矩陣L使A -LC所有的特徵值都具有嚴格的負實部，則線性狀態方程[或者簡單記為矩陣對(A，C)]是可檢的。

基本介紹

• 中文名：可檢性
• 相關詞：能觀的

簡介

已經知道，對於一個能觀的狀態方程，通過適當選擇觀測器增益矩陣任意配置觀測器誤差動態方程特徵值來構造狀態觀測器。由配置這些特徵值的自由度說明可以漸進穩定觀測器誤差動態方程，因此可以說能觀性是通過觀測器增益矩陣漸進穩定觀測器誤差動態方程的充分條件。在狀態方程不能觀的情況下，來研究觀測器誤差動態方程還是不是能漸進穩定的。因此引入了可檢性的概念。將看到可檢性和可鎮定性之間也存在像能觀性和能控性之間類似的對偶關係。首先介紹可鎮定性的例子。狀態方程如下：

狀態方程

其中矩陣對(Al1，C1)確定了一個能觀一維子系統。根據觀測器增益向量L=[Z．，Z。，l3]1，其中很容易選擇觀測器增益￡，來單獨配置能觀子系統的特徵值。根據下三角矩陣塊結構， A-LC的三個特徵值為1+/1，和不能觀子系統的特徵值-1和-2。這樣可以得出結 論，雖然狀態方程是不能觀的，仍然可能構造觀測器增益向量確定一個觀測器，得到由A- LC特徵值確定的漸進穩定的狀態觀測器誤差動態方程。需要強調的是，漸進穩定的觀測 器誤差動態方程可以直接得到，因為不能觀子系統不受觀測器增益向量的影響，從一開始就是漸進穩定的。也看到觀測器增益Z。和Z。不對A-LC的特徵值產生影響。

定義

如果存在一個觀測器增益矩陣L使A -LC所有的特徵值都具有嚴格的負實部，則線性狀態方程(8.1)[或者簡單記為矩陣對(A，C)]是可檢的。
這個定義和先前的特徵值配置結果看到，如果系統是能觀的，那么就是可檢的。另一方面，上述例子說明反之是不成立的。一個狀態方程可以是能檢的，但不一定是能控的，即可鎮定性條件比能控性弱一樣。
上述例子的分析可以推廣如下：如果矩陣對(A，C)是能觀的，那么它就是可檢的，這個已經指出了，所以來看看矩陣對(A，C)不能觀的情況。知道存在坐標變換x(t)一Tz(t)，使得變換後的狀態方程為下圖所示：

方程

其特徵值包括A11一L1C1的特徵值和A22的特徵值。因為(A11，Cl)是能觀矩陣對，因此可以選擇L1使A1l -L1C1的特徵值具有嚴格的負實部。然而，A22不能觀子系統不受觀測器增益矩陣的影響，對於任意的L，A22的特徵值都包括在A- LC的特徵值中。因此，為了使A - LC的每一個特徵值都具有嚴格的負實部，A22的特徵值就必須具有嚴格的負實部。因此我們看到，當矩陣對(A，C)不能觀時，可檢性要求不能觀子系統是漸進穩定的。我們也看到Lz在此分析中沒有起到任何作用。
為了推導和前面可鎮定性類似的可檢性Popov-Belevitch-Hautus代數判據，我們首先建立與能控性和能觀性關係類似的可鎮定性和可檢性之間的正式對偶關係。具體來講，我們可以給出如下命題：矩陣對(A，B)是可鎮定的，若且唯若矩陣對(Ar，Br)是可檢的。矩陣對(A，C)是可檢的，若且唯若矩陣對(AT，CT)是可鎮定的。
對於第一句，如果矩陣對(A，B)是可鎮定的，那么根據定義，存在狀態反饋增益矩陣K，使A-BK的所有特徵值都具有負實部。因為矩陣轉置不影響特徵值，因此(A—BK)T—AT_K7 BT的特徵值也具有嚴格的負實部。將Kr看作是觀測器增益矩陣，可知矩陣對(AT，BT)是可檢的。將上述步驟顛倒，就可以建立逆命題，從而第二句可以用類似的方法討論。

可鎮定性Popov-Belevitch-Hautus判據根據對偶性，可得到可檢性的判據為：

下列命題是等價的：

1．矩陣對(A，C)是可檢的。

2．不存在A的非負實部特徵值對應的右特徵向量和C的所有行正交。

3．對所有具有非負實部的實數A，矩陣訂蘭頁]具有滿列秩。

證明：此定理可由下列的關係來證明：

矩陣對(A，C)是可檢的，若且唯若矩陣對(Ar，CT)是可鎮定的。

存在A的非負實部特徵值對應的右特徵向量和C的所有行正交，若且唯若存在Ar的非負實部特徵值對應的左特徵向量和CT的所有列正交。

套用

如下圖的題目：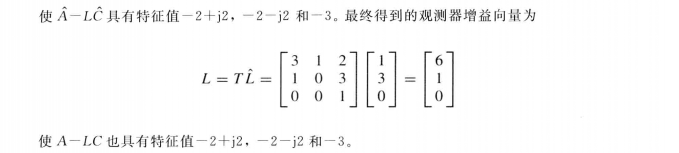

題目

題目

從例題中看到V3 =[2 3 1]T為A的特徵值λ3=-3<0對應的右特徵向量，使CV3 =0。因此可以斷言只有和C正交的A的右特徵向量為V3的純非零倍數，因此也和A3相關。從定理可以得出結論，因為不存在A的非負實部特徵值對應的特徵向量和C的所有行正交，因此狀態方程是可檢的。