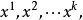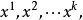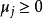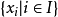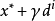最優解

通常定義為不犧牲任何總目標和各分目標的條件下，技術上能夠達到的最好的解。它表示所有的總目標和分目標都可以達到的理想的解。而實際上這樣的解是很少存在的。工程問題固有的內在因素總是包含各種矛盾的，由於科學水平的限制，很多設計因素和系統的約束還不是很了解;許多判別準則。例如： 社會上的相互關係、生活的質量、生態學，以及興趣、愛好等等，是不容易確定的，更不容易定量化。而工程系統的設計問題或規劃問題中勞動力、設備、財力以及時間總是有限的。所以，最最佳化過程只是產生一個在設計和工藝約束條件下所能達到的“最令人滿意解”。

基本介紹

• 中文名：最優解
• 外文名：optimum solution
• 學科：數學
• 套用領域：數學、統計學

簡介

數學規劃的基本概念之一。指在數學規劃問題中，使目標函式取最小值（對極大化問題取最大值）的可行解。使目標函式取最小值的可行解稱為極小解，使其取最大值的可行解稱為極大解。極小解或極大解均稱為最優解。相應地，目標函式的最小值或最大值稱為最優值。有時，也將最優解和最優值一起稱為相應數學規劃問題的最優解。

線性規劃的最優解不一定只有一個，若其有多個最優解，則所有最優解所構成的集合稱為該線性規劃的最優解域。

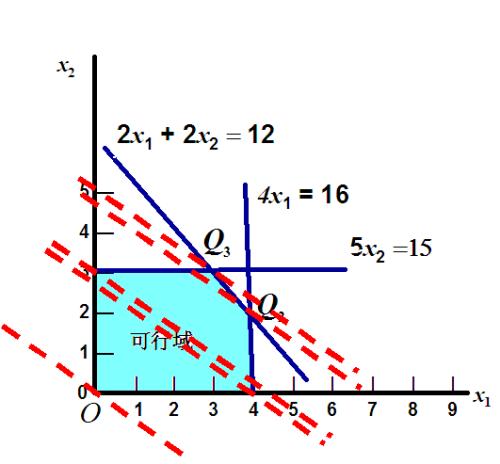
例如:已知變數x，y滿足約束條件：

1、y≤3;

2、x+y≥1;

3、x-y≤1，

則z=2x-y的最優解為（4，3）或（-2，3）；

定理

設D = 非空， 則它的極點集非空且包含有限多個點 而且D 的極方向集非空若且唯若D 無界。若D 無界， 則它的極方向集包含有限個向量 此外， x ∈D 若且唯若x 可以表示為 的凸組合與的非負線性組合之和， 即

其中，，；，

設（SL P）有最優解， 則必存在基最優解（最優極點） ， 記（SL P）的最優極點集為另外， 由(1) 式不難看出，（SL P）有最優解若且唯若對於所有的極方向有。

設 為（SL P） 的最優解， 若D 的某極方向 滿足 （即與c正交） ， 則易見， 對於任意的， 都是最優解。 我們稱滿足的極方向為最優極方向。 記（SL P）的最優極方向集為。

判定方法

最小二乘法估計

最小二乘法估計是建立在模型服從高斯分布的假設之上。當從模型總體隨機抽取M組樣本觀測值後，最合理的參數估計值應該使得模型能最好地擬合樣本數據，也就是估計值和觀測值之差的平方和最小。而對於最大似然估計，當從模型總體隨機抽取M組樣本觀測值後，最合理的參數估計值應該使得從模型中抽取該M組樣本觀測值的機率最大。

最大似然估計

最大似然估計代表了頻率派的觀點：參數雖然未知但是客觀存在的，當參數求出來後，x，y也就知道了。

假設我們觀察的變數是x，觀察的變數取值（樣本）為，要估計的模型參數是θ，x的分布函式是。那么最大似然函式就是θ的一個估計值，它使得事件發生的可能性最大：

通常認為x是獨立同分布的：

所以最大似然估計的一般求解流程就是：

最大似然估計中，參數θ是一個固定的值，只要能夠擬合樣本數據就可以了。但是當樣本過少的時候就容易出現過擬合現象，會得到諸如只要沒見過飛機相撞，飛機就一定不會相撞的扭曲事實。

貝葉斯估計

貝葉斯派將參數θ作為隨機變數，服從某一分布。正因為參數是不固定的，對於給定的x無法用確定的y來表示，而是用機率的方式來表達。

我們希望求出觀察到樣本x的情況下，θ的分布情況。根據貝葉斯定理可得：

上面的後驗機率通常是很難計算的，因為要對所有的參數進行積分，而且，這個積分其實就是所有θ的後驗機率的匯總，其實它是與最優θ是無關的，而我們只關心最優θ（相同）。在這種情況下，我們採用了一種近似的方法求後驗機率，這就是最大後驗估計：

最大後驗估計相比最大似然估計，只是多了一項先驗機率，它正好體現了貝葉斯認為參數也是隨機變數的觀點，在實際運算中通常通過超參數給出先驗分布。最大似然估計其實是經驗風險最小化的一個例子，而最大後驗估計是結構風險最小化的一個例子。如果樣本數據足夠大，最大後驗機率和最大似然估計趨向於一致，如果樣本數據為0，最大後驗就僅由先驗機率決定。儘管最大後驗估計看著要比最大似然估計完善，但是由於最大似然估計簡單，很多方法還是使用最大似然估計。