布爾環

在數學中，布爾環 R 是對於所有 R 中的 x 有 x^2=x 的環，就是說 R 由冪等元素組成。這些環引發自布爾代數。

基本介紹

• 中文名：布爾環
• 外文名：boolean ring
• 套用學科：數學
• 來源：布爾代數
• 性質：布爾環的任何子環是布爾環
• 定義：是對於所有R中x有x^2=x的環

例子

一個例子是任何集合 X 的冪集，在這個環中：0 是空集，1 是全集，加法是對稱差，乘法是交集。另一個例子我們考慮 X 的所有有限子集的集合，運算還是對稱差和交集。更一般的說通過這些運算任何集合域都是布爾環。通過 Stone布爾代數表示定理所有布爾環都同構於一個集合域(作為帶有這些運算的環處理)。

與布爾代數

如果定義

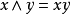
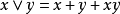
則它們滿足在布爾代數中交、並和補的所有公理。所以每個布爾環都成為了布爾代數。類似的，通過如下定義布爾代數成為了布爾環：

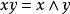
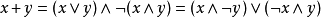
在兩個布爾環之間的映射是環同態，若且唯若它是相應的布爾代數的同態。進一步的，布爾環的子集是環理想(素環理想，極大環理想)，若且唯若它是相應的布爾代數的理想(素理想，極大理想)。布爾環模以環理想的商環對應於相應的布爾代數模以相應的理想的商代數。

性質

所有布爾環 R 滿足對於所有 R 中的 x 有 x + x = 0；因此 -x = x，所有元素都是自身的加法逆元，在布爾環中使用減號沒有意義。因為我們知道

x + x = (x + x) ²= x²+ 2x² + x²= x + 2x + x = x + x + x + x並且因為 <R,+> 是阿貝爾群，我們可以從這個等式的兩端減去 x + x，這給出了 x + x = 0。類似的證明證實了布爾環是可交換的:

x + y = (x + y)² = x²+ xy + yx + y² = x + xy + yx + y而這產生了 xy + yx = 0，它意味著 xy = −yx = yx (使用上面第一個性質)。

x + x = 0 的性質證實了布爾環是在帶有兩個元素的域 F₂ 上的結合代數，但只在這個方向上。特別是，任何有限布爾環都有二的冪的勢。不是所有的在 F₂ 上的單作結合代數都是布爾環: 比如多項式環 F₂[X]。

任何布爾環 R 模以任何環理想 I 的商環 R/I 也是布爾環。類似的，布爾環的任何子環是布爾環。

在布爾環 R 中所有素環理想 P 是極大環理想: R/P 的商環是整環並其同時是布爾環，所以它必定同構於域 F₂，這證實了 P 的極大性。因為極大環理想總是素環理想，我們得出素環理想和極大環理想在布爾環中是一致的。