基本介紹
定義
例子
反例
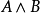

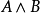

在數學中,完全布爾代數是所有子集都有上確界的布爾代數。...... 在數學中,完全布爾代數是所有子集都有上確界的布爾代數。完全布爾代數在力迫理論中有重要作用。...
布爾代數起源於數學領域,是一個用於集合運算和邏輯運算的公式:〈B,∨,∧,¬ 〉。其中B為一個非空集合,∨,∧為定義在B上的兩個二元運算,¬為定義在B上的...
值得特別注意的是,這個概念在特定的情況下也套用於完全布爾代數,完全格和完全偏序。並且一個有序域被稱為完全的,如果它的任何在這個域中有上界的非空子集,都有...
完全格一定不能混淆於完全偏序(cpo),它構成嚴格的更加一般的一個偏序集合類別。更特殊的完全格是完全布爾代數和完全Heyting代數(locale)。...
給定一個完全布爾代數B,有一個指示為V的布爾值模型,它是馮·諾伊曼全集V的布爾取值的類似者。(嚴格的說,V是真類,所以我們需要適當的重新解釋對於模型意味著什麼...
事實上,通過對布爾代數適當的限制(要求布爾代數完全),可以證明V `},滿足ZFC系統的所有公理,從而構成ZFC系統的一個模型,這樣就避免了科恩方法中利用兼納集構造兼納...
布爾代數的運算規則與集合代數的運算規則是完全相同的。布爾乘法為集合代數中的交集,亦即表示邏輯積關係,布爾加法為集合代數中的並集,亦即表示邏輯和關係。...
定義介紹 完全可分配性(completely distributivity)可分配律的推廣.對於任意兩個集合s和W,用sw表示由W到s中的所有映射的集合.給定一個由Wxs到布爾代數B的映射,它...
在數學裡,海廷代數是一特殊的偏序集,經由廣義化布爾代數而成,得名於阿蘭德·海廷。海廷代數是作為直覺主義邏輯的模型而產生的,是一種排中律不總是成立的邏輯。...
事件代數(event algebra)是一種特殊的布爾代數,設P(Ω)是適合某種條件的所有事件的全體,Ω與∅分別是必然事件與不可能事件,∪,∩,-分別是事件的和、積、逆...
在數學中,Heyting代數是構成對布爾代數的推廣的特殊的偏序集。Heyting代數為直覺邏輯而提出,它是在其中排中律一般不成立的邏輯。完全Heyting代數是無點拓撲學研究的...
布爾素理想定理(Boolean prime ideal theorem)即保證在給定的抽象代數中特定類型之子集的存在性之數學定理。布爾素理想定理聲稱在布爾代數中的理想可以被擴展成素理想...
值得特別注意的是,這個概念在特定的情況下也套用於完全布爾代數(complete Boolean algebra),完全格(complete lattice)和完全偏序(complete partial order)。並且一個有...
就如Stone空間和布爾代數之間有對偶性,Stonean空間和完全布爾代數範疇也有對偶性。 一個極端不連通的第一可數集體豪斯多夫空間(例如度量空間)必定是離散空間。...
