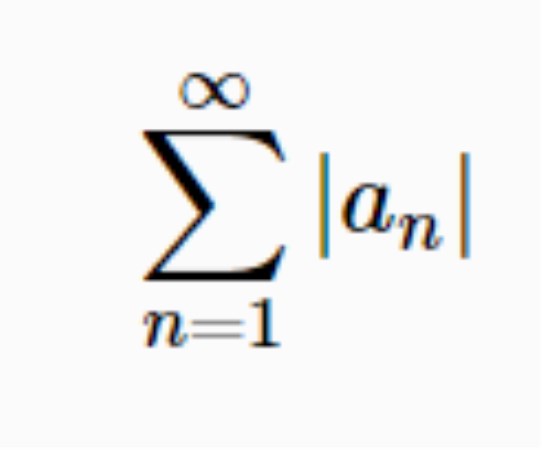逐點絕對收斂指在集合中每一點絕對收斂,設函式列{fn(x)}中每個fn均定義在集A上,若對每個x∈A,序列{fn(x)}∞n=1絕對收斂,即{|fn(x)|}收斂,則稱{fn}在A上逐點絕對收斂。類似地,可對函式項級數及含參數廣義積分引進這個概念。
基本介紹
- 中文名:逐點絕對收斂
- 所屬學科:數學(數學分析)
- 簡介:在集合中每一點絕對收斂
- 相關概念:絕對收斂,逐點收斂
基本介紹,相關概念,函式列的逐點收斂,函式項級數的逐點收斂,絕對收斂級數,
基本介紹
逐點絕對收斂指在集合中的每一點都絕對收斂,設函式列{fn(x)}中每個fn均定義在集A上,若對每個x∈A,序列 絕對收斂,即{|fn(x)|}收斂,則稱{fn}在A上逐點絕對收斂。類似地,可對函式項級數及含參數廣義積分引進這個概念。
絕對收斂,即{|fn(x)|}收斂,則稱{fn}在A上逐點絕對收斂。類似地,可對函式項級數及含參數廣義積分引進這個概念。

相關概念
函式列的逐點收斂
函式列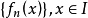 ,若對
,若對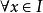 ,數列
,數列 都收斂,則稱函式列在區間I上逐點收斂,記f(x)=
都收斂,則稱函式列在區間I上逐點收斂,記f(x)=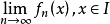 ,稱f(x)為
,稱f(x)為 的極限函式,簡記為
的極限函式,簡記為
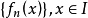
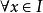

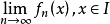


逐點收斂的ε—N定義:對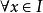 ,及
,及 ,
,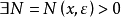 ,當n>N時,恆有
,當n>N時,恆有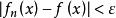 。
。
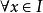

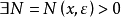
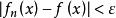
函式項級數的逐點收斂
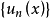
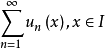
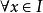
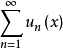
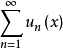
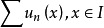
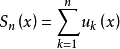
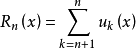
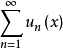
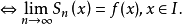
絕對收斂級數
絕對收斂級數指各項取絕對值以後收斂的級數,即若級數