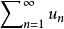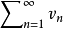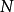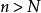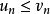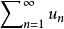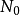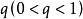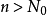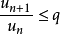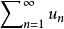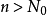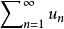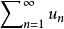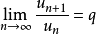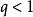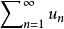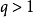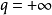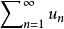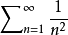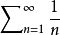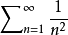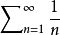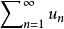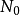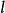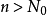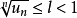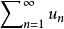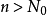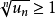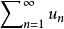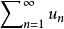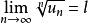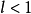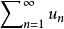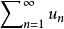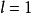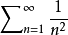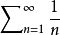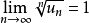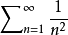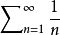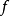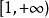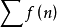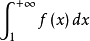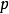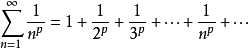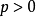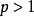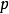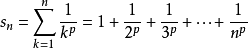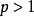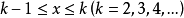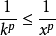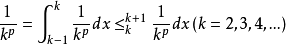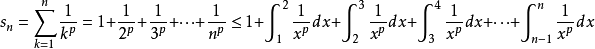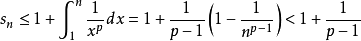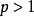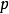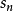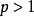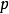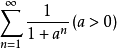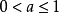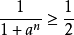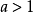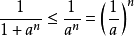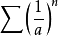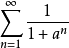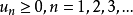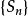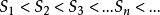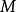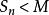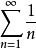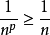正項級數

正項級數，是一種數學用語。在級數理論中，正項級數是非常重要的一種，對一般級數的研究有時可以通過對正項級數的研究來獲得結果，就像非負函式廣義積分和一般廣義積分的關係一樣。所謂正項級數是這樣一類級數：級數的每一項都是非負的。正項級數收斂性的判別方法主要包括：利用部分和數列判別法、比較原則、比式判別法、根式判別法、積分判別法以及拉貝判別法等。

基本介紹

• 中文名：正項級數
• 外文名：Positive series
• 定義：各項都是由正數組成的級數
• 重要級數：p級數
• 收斂性判別：比較原則、比式判別、根式判別
• 套用學科：數學分析

定義

若數項級數各項的符號都相同，則稱它為同號級數。對於同號級數，只需研究各項都是由正數組成的級數，稱它為正項級數。如果級數的各項都是負數，則它乘以-1後就得到一個正項級數，它們具有相同的斂散性。

換句話說，若 ，則稱級數 為正項級數。

收斂性判別

部分和數列判別法

正項級數的部分和數列 是單調增加的數列即： ， 收斂的充要條件是有界，因此有：

正項級數 收斂的充要條件是：它的部分和數列 有界，即存在某正數 ，對於一切正整數 有 。

比較原則

設 和 是兩個正項級數，如果存在某正數 ，使得對一切 都有 ，則有：

（1）若級數 收斂，則級數 也收斂；

（2）若級數發散，則級數也發散。

比式判別法（達朗貝爾判別法）

設 為正項級數，且存在某正常數 及常數 。

（1）若對一切 ，成立不等式 ，則級數 收斂；

（2）若對一切 ，成立不等式 ，則級數 發散。

比式判別法的極限形式：

設 為正項級數，且 ，則有：

（1）當 時，級數 收斂；

（2）當 或 時，級數 發散。

注意：若 ，這時用比式判別法不能對級數的斂散性做出判別，因為它可能是收斂的，也可能是發散的，例如級數 和 ，他們的比式極限都是 ，但 是收斂的， 卻是發散的。

根式判別法（柯西判別法）

設 為正項級數，且存在某正常數 及正常數 。

（1）若對一切 ，成立不等式 ，則級數 收斂；

（2）若對一切 ，成立不等式 ，則級數 發散；

柯西判別法的極限形式：

設 為正項級數，且 ，則：
（1）當 時，級數 收斂；

（2）當 ，級數 發散。

注意：若 ，這時用根式判別法不能對級數的斂散性做出判別，因為它可能是收斂的，也可能是發散的，例如級數 和 ，他們的比式極限都是 ，但 是收斂的， 卻是發散的。

積分判別法

積分判別法是利用非負函式的單調性和積分性質，並以反常積分為比較對象來判斷正項級數的斂散性。

設 為 上非負減函式，那么正項級數 與反常積分 同時收斂或同時發散。

典例

p級數

討論 級數 的收斂性，其中常數 。

解：分兩種情況討論，

（1）當 ， 級數的各項大於等於調和級數 的對應項，即 ，由於調和級數發散，因此根據比較判別法可知，此時 級數發散。

（2）當 時，記 級數的部分和為： .

當 時，取 ，則有 ，所以有：

從而

即有 。

這表明當時， 級數的部分和有界。因此，當時，級數收斂。

例2

討論正項級數的斂散性。

解：

（1）當時，對一切都有，因此級數發散。

（2）當時，對一切都有，而為收斂的等比數列，因此級數收斂。