根值判別法,又稱柯西判別法,是判斷正項級數收斂性的一種重要方法。正項級數收斂性判別法主要有根式判別法、比式判別法、阿貝爾判別法、積分判別法和對數判別法等。
級數收斂的定義,根式判別法,定理 (根式判別法),推論1(根式判別法的極限形式),推論2,根式判別法的局限性,
級數收斂的定義
設有數列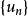 ,此數列的項依次用加號連線起來,即
,此數列的項依次用加號連線起來,即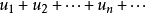 ,或
,或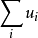 ,稱為數值級數,其中
,稱為數值級數,其中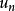 稱為級數的第
稱為級數的第 項或通項,取級數前
項或通項,取級數前 項的和為
項的和為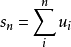 ,稱為級數的
,稱為級數的 項部分和。若級數的部分和數列
項部分和。若級數的部分和數列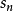 收斂,稱此級數收斂,否則,稱該級數發散。
收斂,稱此級數收斂,否則,稱該級數發散。
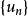
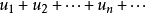
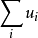
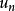


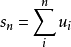

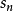
根式判別法
定理 (根式判別法)
有正項級數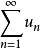 ,存在常數
,存在常數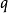 及
及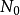 ,
,
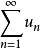
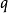
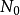
1)若對一切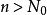 ,成立不等式
,成立不等式
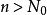
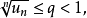
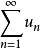
2)若對一切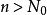 ,成立不等式
,成立不等式
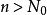
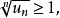
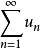
證明:由1)中條件有
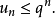
因為上式右邊等比級數當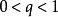 時收斂,故由比較原則,這時有級數
時收斂,故由比較原則,這時有級數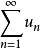 也收斂。對於情形 2),由條件可以推出
也收斂。對於情形 2),由條件可以推出
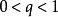
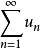
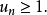
推論1(根式判別法的極限形式)
設有正項級數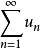 ,且
,且
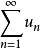
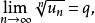
1)當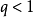 時,級數
時,級數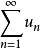 收斂。
收斂。
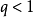
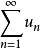
2)當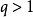 時,級數
時,級數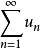 發散。
發散。
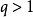
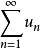
推論2
設有正項級數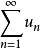 ,且
,且
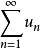
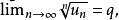
則
1)當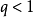 時,級數
時,級數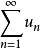 收斂。
收斂。
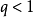
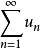
2)當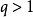 時,級數
時,級數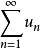 發散。
發散。
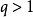
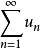
根式判別法的局限性
根式判別法本質上還是比較判別法,是將級數和幾何級數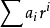 比較得到的,是在正項級數斂散性判別中是一個十分重要的方法,不少級數均可依此法判別其斂散性。
比較得到的,是在正項級數斂散性判別中是一個十分重要的方法,不少級數均可依此法判別其斂散性。
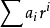
從理論上來說,凡是能用比式判別法判斷其斂散性的級數,必定也能用根式判別法來判斷其斂散性,但反之不成立。這說明根式判別法較比較判別法有更大的適用性,但是,根式判別法也有其失效性。在根式判別法只討論了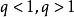 的情況,並沒有考慮
的情況,並沒有考慮 的情況,也沒有考慮
的情況,也沒有考慮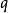 不存在又是怎樣的情況。例如
不存在又是怎樣的情況。例如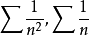 都有
都有
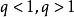

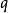
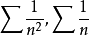
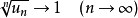
但前者收斂,後者發散。這說明這種判別法存在著一定的不足。
