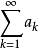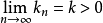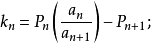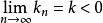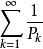庫默爾判別法

庫默爾判別法(Kummer's discriminant method)亦稱迪尼-庫默爾判別法，是正項級數收斂性判別法之一，德國數學家庫默爾(Kummer)在1835年給出了一個判別法，且是充要條件。達朗貝爾判別法、拉貝判別法、伯爾特昂判別法均可作為庫默爾判別法的推論。

基本介紹

• 中文名：庫默爾判別法
• 外文名：Kummer's discriminant method
• 別稱：迪尼-庫默爾判別法
• 所屬學科：數學
• 提出者：庫默爾(Kummer)
• 簡介：正項級數收斂性判別法之一

基本介紹

關於正項級數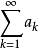(a_k≥0)的收斂法則，德國數學家庫默爾(Kummer)在1835年給出了一個判別法，且是充要條件。

庫默爾判別法

(1)設正項級數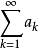收斂，若且唯若存在正項級數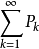及實數c>0，使得

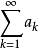
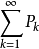
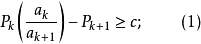
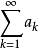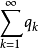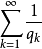(2)設正項級數發散，若且唯若存在正項級數使得發散，且

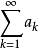
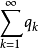
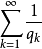
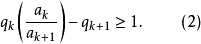
庫默爾判別法的極限形式

庫默爾判別法的極限形式：

(1)若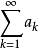(a_k>0)收斂，若且唯若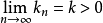，這裡P_n>o，且

(2)若(a_k>0)發散，若且唯若，這裡P_n>0，發散，k_n仍由上式給出。從庫默爾判別法不難看出，達朗貝爾判別法、拉貝判別法、伯爾特昂判別法均可作為它的推論。