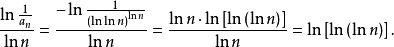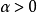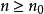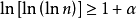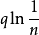對數判別法(logarithmic test)是正項級數收斂性的一種判別法,是以∑n-p,∑(nlnpn)-1為比較級數得到的判別正項級數∑an收斂性的方法。第一對數判別法:若存在p,使n充分大時Ln=(ln(1/an))/ln n≥p>1,則∑an收斂;若n充分大時Ln≤1,則∑an發散;第二對數判別法:設Ln=|ln(nan)|/lnln n,結論同上。
基本介紹
- 中文名:對數判別法
- 外文名:logarithmic test
- 所屬學科:數學(數學分析)
- 簡介:正項級數收斂性的一種判別法
基本介紹,對數判別法的證明,例題解析,
基本介紹
第一對數判別法:若存在p,使n充分大時
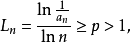
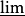
第二對數判別法:設Ln=|ln(nan)|/lnln n,結論同上。
對數判別法的證明
設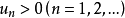 ,且
,且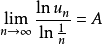 ,試證明:當0<A<1時,級數
,試證明:當0<A<1時,級數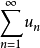 發散;當A>1時,級數
發散;當A>1時,級數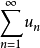 收斂。
收斂。
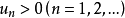
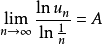
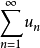
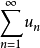
證明 因為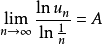 ,所以任給ε>o,存在正整數N,當n>N時,有
,所以任給ε>o,存在正整數N,當n>N時,有
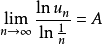
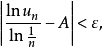
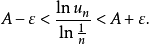
當0<A<1時,取ε>0,使A+ε=q<1,於是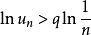 。即
。即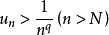 ,而
,而 發散,所以
發散,所以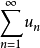 發散;
發散;
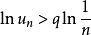
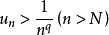

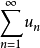
當A>1時,取ε>0,使A-ε=p>1,於是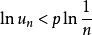 ,即
,即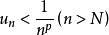 ,而
,而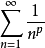 收斂,所以
收斂,所以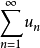 收斂。
收斂。
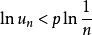
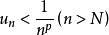
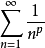
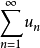
例題解析
利用對數判別法研究如下通項的級數的收斂性:
【例1】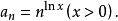
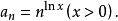
解利用對數判別法,因為:
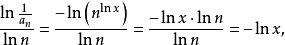
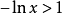
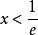
【例2】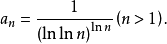
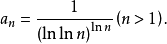
解利用對數判別法: