基本介紹
- 中文名:面渦
- 外文名:Vortex sheet
- 領域:流體力學
- 套用場合:表面流速
- 理論基礎:柯西主值積分
- 相似詞:渦環
定義,帶周期性邊界,
定義
為滿足流體壁面無滑移條件,在壁面上產生一個切向速度的間斷面(面渦),使流體通過面渦從速度U降為0。
當渦量集中在薄層內部,而薄層表面積要比薄層厚度大得多時,可以把這個薄層抽象為面渦。
面渦強度定義:γ=lim∫ωdn
因此面渦在數學上可看成為內嵌於無黏流場中的間斷面。
同時面渦是個物質面。
在雷諾數高的情況下,面渦往往不穩定。特別是它們可能表現出開爾文 - 亥姆霍茲不穩定性。
渦旋片運動方程式由復坐標z = x + iy給出。該表由z(s,t)} 參數描述,其中 s是坐標,z與參考點之間的長度, t是時間。讓 gamma(s,t)表示面渦的強度,即切向不連續性中的跳躍。然後由該面引起的速度場是:
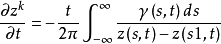
帶周期性邊界
可以使用在流動方向上具有周期邊界的平坦面渦來建立高雷諾數下的時間自由剪下層。 讓我們假設周期邊界之間的間隔是1的距離。然後渦旋片的運動方程減少。
注意,上述等式的積分是柯西主值積分。具有恆定強度的平面渦旋片的初始條件是 z(Gamma,0)= Gamma。平渦旋片是平衡溶液。然而,對於具有無窮小周期性干擾。線性理論表明傅立葉係數 A_ k以與k成比例的比例成指數增長。也就是說,傅立葉模式的波數越高,其增長越快。然而,線性理論不能超出初始狀態。如果考慮非線性相互作用,漸近分析表明,對於大的k和有限t <t_ c,其中t_c是臨界值,傅立葉係數A_ k呈指數衰減。面渦解決方案預計在關鍵時刻失去分析性。
由Birkoff-Rott方程給出的渦流片解決方案不能超越關鍵時刻。渦流片中分析性的自發損失是數學建模的結果,因為具有粘度的實際流體(不管如此小)將永遠不會發展出奇點。粘度在實際流體中起到平滑或正則化參數的作用。已經對渦旋片進行了廣泛的研究,其中大部分是通過離散或點渦近似,具有或不具有去斑紋化。使用點渦近似和δ正則化Krasny(1986)獲得渦旋片平滑捲曲成雙分支螺旋。由於點旋渦本身是混沌的,所以需要傅立葉濾波器來控制捨入誤差的增長。通過具有循環密度的電弧擴散的渦流面板連續近似渦旋片也表明片材捲起成雙分枝螺旋。
在許多工程和物理套用中,時間自由剪下層的生長是令人感興趣的。自由剪下層的厚度通常通過動量厚度測量。動量厚度具有長度的尺寸,非尺寸動量厚度由theta_ ND = θ/ L給出。動量厚度可用於測量渦流層的厚度。

