對數容量

對數容量(logarithmic capacity)是由對數核確定的一種容量。在R中，關於對數核考慮緊集F的倒容量W_l(F)，當限制F包含於單位圓B內時，若W_l(F)>0，則把1/W_l(F)稱為F的維納容量。

基本介紹

• 中文名：對數容量
• 外文名：logarithmic capacity
• 領域：數學
• 學科：位勢論
• 性質：容量
• 定義：由對數核確定的一種容量

概念

對數容量(logarithmic capacity)是由對數核確定的一種容量。在R中，關於對數核考慮緊集F的倒容量W_l(F)，當限制F包含於單位圓B內時，若W_l(F)>0，則把1/W_l(F)稱為F的維納容量。對一般緊集F，W_l(F)可能取0值或負值，要做類似的處理不方便，故定義：

為F的對數容量.對F⊂B，兩種容量值相差甚大，但兩種零容集等價，都是全不連通的勒貝格零集。值得注意的是，包含於區間[0，1]的康托爾三分集是勒貝格零集，但具有正的對數容量。當C_l(F)>0時，對R\F的無界分支上以無窮遠點為極的格林函式g(z，∞)，極限

存在，稱為魯賓常數，它正好等於W_l(F)。

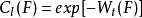
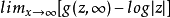
容量

容量是刻畫巴拿赫空間中緊集的“大小”或“粗細”的一個不變數。設X是巴拿赫空間，A是X的一個緊子集。‖x‖是x∈X的範數，是給定的正數，y₁，y₂，…，y_m是A中的m個點，如果它們中每兩點之間的距離都超過ε，也即i≠k(i，k=1，2，…，m)時ρ(y_i，y_k)=‖y_i-y_k‖>ε，則稱點組{y_k}_k=1是ε-分離的.自然，對給定的ε>0，ε-分離的點組{y_k}_k=1的點的個數與這些點的取法有關。但其最大值M_ε(A)=maxm卻是集A的一個不變數，C_ε(A)=logM_ε(A)稱為A的容量。C_ε(A)關於A是單調遞增的而關於ε則是單調遞減的.在函式逼近論中，主要是對一些函式類考慮其容量在ε→0時的漸近性態及其套用。它開始於20世紀50年代。

容量與熵之間有如下關係：若X是巴拿赫空間，A是X的緊子集，則對ε>0有不等式：

其中C_ε(A)是A的容量，H_ε(A)是A的熵，H_ε(A)是A關於X的熵。

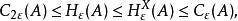
對數位勢

對數位勢是一般位勢的經典模型之一。在R中，以K(x，y)=-log|x-y|為核(稱為對數核)的位勢稱為對數位勢，記為U_l。對數核是對稱的、平移不變的，但不是正核.二維引力場的位勢即為對數位勢。

位勢論

現代分析數學領域的一個分支，主要研究各種形式的位勢(函式)和與其密切關聯的調和函式、上(下、超、次)調和函式族的各種性質及其套用。經典位勢論的主要研究工具是微積分，並與微分方程、複變函數論緊密關聯;現代位勢論以拓撲、泛函分析與測度論、廣義函式等為主要工具，與分析數學領域的諸多分支相互滲透並和隨機過程建立了深刻的內在聯繫。位勢論起源於物理學的萬有引力學說和靜電學，遠在1733年，拉格朗日(Lagrange，J.-L.)就注意到引力場是一個函式(稱為牛頓位勢)的梯度。

1925年，里斯(Riesz，F.)引進了上(下)調和函式的概念，為位勢論研究提供了新的方法；里斯分解定理建立了上調和函式與位勢之間的緊密聯繫；而對上調和函式連續性的研究導致了細拓撲概念的引入。

20世紀30年代，瓦萊·普桑(Vallée-Poussin，C.-J.-G.-N.de la)用現代觀點改進並發展了龐加萊掃除法；弗羅斯特曼(Frostman，O.)發展了高斯變分法，成功地解決了緊集的平衡問題和掃除問題。同期，位勢論已推廣到非古典核的情況，特別是里斯位勢核，它已不屬於通常與偏微分方程關聯的位勢核了。

從20世紀40年代起，泛函分析、拓撲學的方法被系統地引入位勢論並使它發展到一個新水平。1941年，嘉當(Cartan，H.)利用希爾伯特空間理論研究具有有限能量的測度等，得到很大成功；同年，馬丁(Martin，R.S.)建立了馬丁邊界理論，導致了關於一般理想邊界的深入研究；1950年，戴尼(Deny，J.)用廣義函式論解決了完備化問題;1955年，紹凱(Choquet，G.)建立了一般容量理論及可容性定理，並用凸錐極端點理論改進了馬丁的成果.此外，對於更一般空間(例如流形、LCA群)和更一般位勢核的位勢論也有了深入的探討。

近30多年來，位勢論迅速發展，其顯著特點之一是各種公理體系的建立.為統一處理已有的理論並加以推廣使之適用於一般橢圓型和拋物型方程或隨機過程，自20世紀50年代中期起，陶茨(Tautz，G.)、杜布(Doob，J.L.)、布雷洛、鮑爾(Bauer，H.)、邦尼(Bony，J.M.)、康斯坦丁斯庫(Constantinescu，C.)和柯尼(Cornea，A.)等人分別提出了不同的公理系統，建立各種形式的調和空間位勢論(最近，關於多重調和空間及非線性位勢論的公理系統也先後建立起來)；而戴尼和博靈(Beurling，A.)等人則從能量和狄利克雷積分等概念出發建立了狄利克雷空間論。位勢論發展的另一個顯著特點是，越來越廣泛深入地與相鄰分支，如複分析(包括黎曼曲面)、拓撲學、幾何測度論、微分幾何、微分方程、調和分析等相互結合和滲透，且發揮日益明顯的作用與影響。特別引人注目的是，對於它與隨機過程論之深刻聯繫的深入研究，同時促進了這兩個分支的繁榮和發展，在杜布、亨特(Hunt，G.A.)、邁耶(Meyer，P.A.)和鐘開萊等人出色工作的基礎上，產生了所謂機率位勢論或馬爾可夫過程位勢論，與此有關的課題正吸引著大批學者去做深入研究。