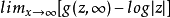魯賓常數

當Cl(F)>0時，對R\F的無界分支上以無窮遠點為極的格林函式g(z,∞)，極限存在，稱為魯賓常數，它正好等於W_l(F)。

基本介紹

• 中文名：魯賓常數
• 外文名：Rubin constant
• 適用範圍：數理科學

簡介

對數容量

對數容量是由對數核確定的一種容量。

在R中，關於對數核考慮緊集F的倒容量W_l(F)，當限制F包含於單位圓B內時，若W_l(F)>0，則把1/W_l(F)稱為F的維納容量。對一般緊集F，W_l(F)可能取0值或負值，要做類似的處理不方便，故定義：

為F的對數容量。

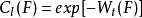
對F⊂B，兩種容量值相差甚大，但兩種零容集等價，都是全不連通的勒貝格零集。值得注意的是，包含於區間[0，1]的康托爾三分集是勒貝格零集，但具有正的對數容量。

定義

當C_l(F)>0時，對R\F的無界分支上以無窮遠點為極的格林函式g(z,∞)，極限

存在，稱為魯賓常數，它正好等於W_l(F)。

格林函式

在數學中，格林函式是一種用來解有初始條件或邊界條件的非齊次微分方程的函式。在物理學的多體理論中，格林函式常常指各種關聯函式，有時並不符合數學上的定義。

從物理上看，一個數學物理方程是表示一種特定的"場"和產生這種場的"源"之間的關係。例如，熱傳導方程表示溫度場和熱源之間的關係，泊松方程表示靜電場和電荷分布的關係，等等。