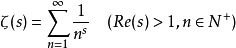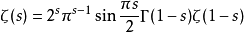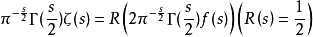起源
黎曼猜想是
波恩哈德·黎曼1859年提出的,這位數學家於1826年出生在當時屬於
漢諾瓦王國的名叫布列斯倫茨的小鎮。1859年,黎曼被選為了
柏林科學院的通信院士。作為對這一崇高榮譽的回報,他向柏林科學院提交了一篇題為“論小於給
定數值的
素數個數”的論文。這篇只有短短八頁的論文就是黎曼猜想的“誕生地”。
黎曼那篇論文所研究的是一個數學家們長期以來就很感興趣的問題,即
素數的分布。素數又稱質數。質數是像2、5、19、137那樣大於1且除了1和自身以外不能被其他
正整數整除的自然數。這些數在數論研究中有著極大的重要性,因為所有大於1的正整數都可以表示成它們的合。從某種意義上講,它們在
數論中的地位類似於物理世界中用以構築萬物的
原子。質數的定義簡單得可以在中學甚至國小課上進行講授,但它們的分布卻奧妙得異乎尋常,數學家們付出了極大的心力,卻迄今仍未能徹底了解。
黎曼論文的一個重大的成果,就是發現了質數分布的奧秘完全蘊藏在一個特殊的函式之中,尤其是使那個函式取值為零的一系列特殊的點對質數分布的細緻規律有著決定性的影響。那個函式如今被稱為
黎曼ζ函式,那一系列特殊的點則被稱為黎曼ζ函式的非平凡零點。
有意思的是,黎曼那篇文章的成果雖然重大,文字卻極為簡練,甚至簡練得有些過分,因為它包括了很多“證明從略”的地方。而要命的是,“證明從略”原本是應該用來省略那些顯而易見的證明的,黎曼的論文卻並非如此,他那些“證明從略”的地方有些花費了後世數學家們幾十年的努力才得以補全,有些甚至直到今天仍是空白。但黎曼的論文在為數不少的“證明從略”之外,卻引人注目地包含了一個他明確承認了自己無法證明的命題,那個命題就是黎曼猜想。黎曼猜想自1859年“誕生”以來,已過了160個春秋,在這期間,它就像一座巍峨的山峰,吸引了無數數學家前去攀登,卻誰也沒能登頂。
有人統計過,在當今數學文獻中已有超過一千條數學命題以黎曼猜想(或其推廣形式)的成立為前提。如果黎曼猜想被證明,所有那些數學命題就全都可以榮升為定理;反之,如果黎曼猜想被否證,則那些數學命題中起碼有一部分將成為陪葬。
具體內容
黎曼觀察到,素數的
頻率緊密相關於一個精心構造的所謂黎曼zeta函式ζ(s)的性態。黎曼假設斷言,方程ζ(s)=0的所有有意義的解都在一條直線上。這點已經對於開始的1,500,000,000個解驗證過。
之所以要對這一表達式進行解析延拓, 是因為這一表達式只適用於
複平面上 s 的實部 Re(s) > 1 的區域 (否則
級數不
收斂)。黎曼找到了這一表達式的
解析延拓(當然黎曼沒有使用 “解析延拓” 這樣的現代
複變函數論術語)。運用
路徑積分,解析延拓後的黎曼ζ 函式可以表示為:
這裡我們採用的是歷史文獻中的記號, 式中的積分實際是一個環繞正實軸進行的圍道積分(即從 +∞ 出發, 沿
實軸上方積分至原點附近, 環繞
原點積分至實軸下方, 再沿實軸下方積分至 +∞ ,而且離實軸的距離及環繞原點的半徑均趨於 0),按照現代數學記號應記成:
其中積分路徑C跟上面所述相同,環繞正實軸,可以形象地這樣表示:

式中的 Γ 函式 Γ(s) 是
階乘函式在複平面上的
推廣, 對於
正整數 s>1:Γ(s)=(s-1)!。可以證明, 這一積分表達式除了在 s=1 處有一個簡單
極點外在整個
複平面上解析。這就是黎曼ζ 函式的完整定義。
運用上面的積分表達式可以證明,黎曼ζ 函式滿足以下代數關係式:
從這個關係式中不難發現,黎曼ζ 函式在 s=-2n (n 為正整數) 取值為零 - 因為 sin(πs/2) 為零。
複平面上的這種使黎曼ζ 函式取值為零的點被稱為黎曼ζ 函式的零點。因此 s=-2n (n 為正整數)是黎曼ζ 函式的零點。這些零點分布有序、 性質簡單, 被稱為黎曼ζ 函式的平凡零點 (trivial zero)。除了這些平凡零點外,黎曼ζ 函式還有許多其它零點, 它們的性質遠比那些平凡零點來得複雜, 被稱為非平凡零點 (non-trivial zeros)。
黎曼ζ 函式的所有非平凡零點都位於複平面上 Re(s)=1/2 的直線上,也即方程ζ(s)=0的解的實部都是1/2。
在黎曼猜想的研究中, 數學家們把
複平面上 Re(s)=1/2 的直線稱為 critical line(
臨界線)。運用這一術語,黎曼猜想也可以表述為:黎曼ζ 函式的所有非平凡
零點都位於 critical line 上。
等價定理
1901年Helge von Koch指出,黎曼猜想與強條件的
素數定理等價。
驗證進展
荷蘭三位數學家J.van de Lune,H.J.Riele te以及D.T.Winter利用
電子計算機來檢驗黎曼的假設,他們對最初的2億個齊打函式的零點檢驗,證明黎曼的假設是對的。他們在1981年宣布他們的結果,目前他們還繼續用電子計算機檢驗底下的一些零點。
1982年11月蘇聯數學家馬帝
葉雪維奇在
蘇聯雜誌《Kibernetika》宣布,他利用電腦檢驗一個與黎曼猜想有關的數學問題,可以證明該問題是正確的,從而反過來可以支持黎曼的猜想很可能是正確的。
1975年
美國麻省理工學院的萊文森在他患癌症去世前證明了No(T)>0.3474N(T)。
1980年
中國數學家樓世拓、
姚琦對萊文森的工作有一點改進,他們證明了No(T)>0.35N(T)。
1932年C.L.Siegel發表的文章中,有下面這樣一個公式:
文章的作者根據這個公式的幾何意義以及
cos函式的零點性質,直接推導出來No(T)=N(T),即證明了區域內的零點全部落在臨界線上。
C.L.Siegel從黎曼的遺稿中共整理出來四個公式,其中有三個公式在文獻和教科書中經常出現,唯獨上面這個公式,80多年來很少有文獻提到它,就連C.L.Siegel本人對於這個公式的作用也大惑不解。實際上,只要跳出解析數論來看黎曼手稿,就能清楚地看到,黎曼用
複分析的幾何思想嚴格地證明了現代所說的“黎曼猜想”。這也許是數學史上最大的冤案。
英國《
每日郵報》2015年11月17日報導,奈及利亞教授奧派耶米 伊諾克(Opeyemi Enoch)成功解決已存在156年的數學難題——黎曼猜想,獲得100萬美元(約合人民幣630萬元)的獎金。
伊諾克博士在奈及利亞某大學任教。他表示,自己在2010年取得關鍵性突破,這為後來能夠解決這一千年難題奠定了基礎。他說,自己之所以決定解決這一著名的數學難題不是為了獎金,而是因為自己的學生。正是因為學生們相信自己,他才開始嘗試解決這一數學難題。
然而,克萊數學研究所既不證實也不否認伊諾克博士正式解決了這一問題,只是簡單表示對這些千年數學難題的解決辦法不予評論。
2018年9月,麥可·阿蒂亞聲明證明黎曼猜想,將於9月24日海德堡獲獎者論壇上宣講。9月24日,麥可·阿蒂亞貼出了他證明黎曼假設(猜想)的預印本。