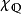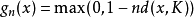貝爾函式

在研究函式的連續性基礎上產生的一類重要的函式。R.L.貝爾於1899年提出如下的函式分類方法：以區間【0,1】上的函式為例，【0,1】上的連續函式稱為0類函式。0類函式序列點點收斂的極限函式，當它不是0類函式時，就稱為1類函式。1類函式序列點點收斂的極限函式，如果不是0類或1類的函式時，便稱為2類函式。依次對每一個自然數n，可以引入n類函式的概念。

基本介紹

• 中文名：貝爾函式
• 外文名：Baire function
• 提出時間：1899年
• 提出者：R.L.貝爾
• 特點：可以引入n類函式的概念
• 學科：數理科學

定義

在數學，貝爾函式是從獲得的連續函式的函式，通過形成的功能序列的逐點限制的操作的超限疊代。它們是由René-Louis Baire於1899年引入的。Baire集是一個特徵函式是Baire函式的集合。

貝爾函式分類

對於任何可數的序數α，α類的貝爾函式形成了在拓撲空間上定義的實值函式的向量空間，如下所示。

• Baire 0類函式是連續函式。
  
• Baire1類函式是那些Baire類0函式序列的逐點限制的函式。
  
• 一般來說，Baire類α函式都是Baire類小於α的函式序列的點函式。
  

一些作者通過從類α的函式中去除小於α的類的所有函式來稍微不同地定義類。這意味著每個Baire函式都有一個定義良好的類，但給定類的函式不再構成一個向量空間。

亨利·勒貝格（Henri Lebesgue）證明了（對於單位區間的函式）每個可數序數的Baire類包含的函式不在任何較小的類中，並且存在不在任何Baire類中的函式。

Baire class 1

例子：

任何微分函式的導數都是1類的。導數不連續（x= 0）的可微函式的一個例子是等於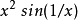 當x≠0時，以及當x= 0時為0。一個無限的相似函式的總和（通過有理數進行縮放和移位）甚至可以給出一個可微函式，其導數在稠密集上是不連續的。然而，它必然具有連續性點，這很容易從Baire表征定理中得到（K=X=R）。

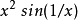
整數集合的特徵函式，如果x是整數，則等於1，否則為0。（無數個大的不連續點）

Thomae函式，無理數x為0，有理數p/q（簡約形式）為1 /q。（一組稠密的不連續性，即有理數的集合。）

康托爾集合的特徵函式，如果x在康托爾集合中，則等於1，否則為0。這個函式對於一組不可數的x值是0，對於不可數組是1。它在任何等於1的地方都是不連續的，在任何等於0的地方都是連續的。它通過連續函式來近似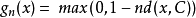 ，在哪裡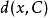 是Cantor集合中距離最近點的距離。

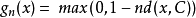
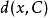
貝爾函式表征定理指出，在分支空間X上定義的實值函式f是Baire-1函式，若且唯若對於X的每個非空封閉子集K，f對K的限制都有一個相對連續點到K的拓撲。

通過Baire的另一個定理，對於每Baire-1功能的連續性的點是comeagerģ_δ集（1995年Kechris，定理（24.14））。

Baire class 2

例子：

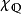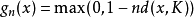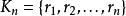不屬於等級1的區間[0,1]上的Baire二類函式的一個例子是有理數的特徵函式， ，也被稱為Dirichlet函式。到處都是不連續的。這可以通過注意到，對於任何有限的理性集合而言，這個集合的指標函式是Baire 1：即函式 同樣收斂於指標函式 ，在哪裡 是理性的有限集合。由於理性是可數的，我們可以看看這些事情的點狀限制 ，在哪裡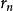 是合理的列舉。根據上述定理，不是Baire-1：不連續點是整個區間。