基本介紹
定義
漢語釋義
數學定義
 序數
序數序數種類
算術
 圖一
圖一 圖二
圖二 圖三
圖三 圖四
圖四 圖五
圖五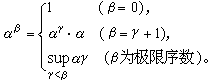 圖六
圖六相關概念
 序數
序數
 序數
序數 圖一
圖一 圖二
圖二 圖三
圖三 圖四
圖四 圖五
圖五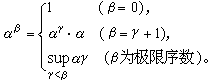 圖六
圖六 序數
序數集合論基本概念之一,是日常使用的第一、第二等表示次序的數的推廣。序數概念是建立在良序集概念之上的,而良序集又是偏序集、全序集的特殊情形。...
序數詞是數詞的一種,主要在英語語法中講到,在漢語中表示為“第幾”。此外,在生日中,描述你出生的日期時,也會用到序數詞。比如:May-first (5月1日) 中文名...
初始序數(initial ordinals number)是一類重要的序數。若序數α不與任何序數β<α等勢,則α稱為初始序數。序數是集合論基本概念之一。是“第一”、“第二”等...
可構造序數(constructive ordinal)是一種特殊的序數。α為可構造序數,是指存在一個記號系統S,使得S中有α的記號。可構造序數都是可數序數,可構造序數的全體構成...
序數理論是數學的一個分支,是使用二元關係(如,大於、優於)來研究順序的直觀概念。它提供了一個用於描述諸如“這小於”或“這在其之前”的語句的正式框架。 本文...
為麻將裡面的牌型,比如說全帶五,麻將術語。每副牌及將牌必須有5的序數牌。不計斷麼。而序數牌就是只一對以上的牌型·就是任何花色都帶有五,包括將牌。...
原子序數(atomic number)是指元素在周期表中的序號。數值上等於原子核的核電荷數(即質子數)或中性原子的核外電子數。例如碳的原子序數是6,它的核電荷數(質子數...
序數加法(addition of ordinals)是序數的一種運算,對任意序數α,β,γ,有:1.α+0=α;2.α+β+=(α+β)+;3.α+γ=sup{α+β|β<γ},當γ是極限...
在經濟學中,序數效用函式(Ordinal Utility Function)是指用於描述一系列從最受偏好到最不受偏好的商品束排列的效用函式。序數效用論1認為,問哪一個選項比另一個更...
在數學中,首個不可數序數,傳統記之為ω1(或有時為Ω),是一個最小的序數,而其於被考慮為集合時為不可數。它是所有可數序數的最小上界。ω1 的所有元素,皆...
序數紀日法。如《梅花嶺記》:“二十五日,城陷,忠烈拔刀自裁。”《項脊軒志》:“三五之夜,明月半牆。…‘三五”指農曆十五日。《〈黃花岡七—十二烈士事...
可構造序數是一種特殊的序數。α為可構造序數,是指存在一個記號系統S,使得S中有α的記號。可構造序數都是可數序數,可構造序數的全體構成序數的一個前節,並且可...
由短周期元素和長周期元素共同構成的族叫做主族。族序數是指短周期元素和長周期元素...
序數紀月法。如《采草藥》:“如平地三月花者,深山中則四月花。”《〈指南錄〉後序》“德祜二年二月”,“是年夏五”,“五”就是五月。《譚嗣同》今年四月,...
序數效用是“基數效用”的對稱。用序數詞 (第一,第二,第三,……) 來表示其相對水平高低的效用。以資產階級經濟學家帕累托等人為代表的序數效用論者認為,效用...
序數回歸(Ordinal 回歸)是一種針對有序尺度因變數數據的回歸方法,一般套用在複雜抽樣過程中。該方法是由McCullagh創立的,能夠利用預測變數(可以是分類型變數和數值型...
序數效用論(Theory Of Ordinal Utility)是為了彌補基數效用論的缺點而提出來的另一種研究消費者行為的理論。...
序數算術包括序數加法、序數乘法、序數方冪、序數除法。...... 序數算術簡介 編輯 序數算術包括序數加法、序數乘法、序數方冪、序數除法。序數算術運算法則 編輯 ...
序數乘法(multiplication of ordinals)是序數的一種運算,對任意序數α,β,γ,有:1.α·0=0;2.α·β+=(α·β)+α;3.α·γ=sup{α·β|β<γ},當...
第一類序數(ordinal number of the first class)一類序數.指有限序數.即滿足α<ω0的序數 ...
序數方冪是序數的一種運算。序數算術實質上不同於基數算術。...... 3、𝞪𝞬=sup{𝞪𝞫|𝞫<𝞬},當𝞬是極限序數時成立。序數方冪舉例 編輯 ...
序數是集合論基本概念之一,是日常使用的第一、第二等表示次序的數的推廣。序數概念是建立在良序集概念之上的,而良序集又是偏序集、全序集的特殊情形。序數類閉...
相對原子質量表是指按照原子序數排列。 本表數據源自最近元素周期表(IUPAC 2005 standard atomic weights),以12C=12為標準。 本表方括弧內的原子質量為放射性元素...
數詞基數變序數 (1)第1至第19一般是在基數詞後加th,但變化特殊的有one—first, two—second, three—third, eight—eighth, nine—ninth, five—fifth, ...
