基本介紹
- 中文名:逐點收斂
- 外文名:Point-by-point convergence
- 分類:數理科學
定義
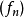
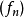
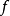

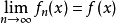
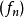
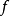
性質
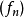
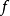
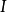
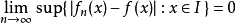
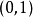

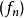
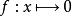
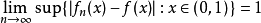
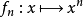
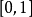
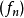
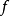
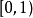
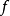
拓撲性質
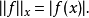
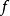
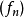
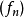
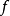

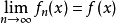
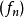
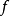
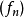
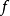
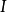
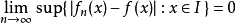
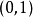

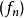
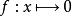
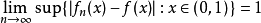
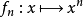
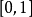
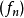
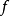
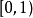
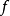
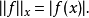
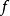
在數學中,逐點收斂(或稱簡單收斂)描述的是一列函式向一個特定函式趨近的現象中的一種。簡單來說,就是對定義域裡的每一點,這個函式列在這點上的取值都趨於一...
我們知道,隨機變數實際上是定義在機率空間上取值為實數的函式,因此我們可以像數學分析時論函式序列逐點收斂性那樣去討論隨機變數序列在每個樣本點處取值的收斂性。...
。接著,設序列的逐點極限為f。也就是說: ,那么,f是 -可測的,且: 。單調收斂定理證明 我們首先證明f是 -可測函式。為此,只需證明區間[0,t]在f下的原像...
數學分析的基本概念之一,它與“有確定的(或有限的)極限”同義,“收斂於……”相當於說“極限是……(確定的點或有限的數)”。在一些一般性敘述中,收斂和收斂...
已知其在一個給定的點集C上收斂得足夠快的某些多項式序列,必在一個把C包含在內的點集上收斂,這個現象就稱為過收斂。...
這是一個單調遞減函式,逐點收斂到函式f:當x屬於[0,1) 時f(x) 等於 0 ,f(1) 等於 1。但這個函式列不是一致收斂的,因為f不連續。...
如果這個函式列逐點收斂到一個連續的函式 ,那么這個函式列一致收斂到 。這個定理以義大利數學家烏利塞·迪尼命名。 對於單調遞減的函式列,定理同樣成立。這個定理是...
其中函式極限是在逐點收斂的意義上的極限,函式取值和積分可以是無窮大。法圖引理驗證推導 編輯 定理證明基於單調收斂定理。設 為函式列的下極限。對每一個正整數 ...
在測度論中,葉戈羅夫定理確立了一個可測函式的逐點收斂序列一致連續的條件。這個定理以俄國物理學家和幾何學家德米特里·葉戈羅夫命名,他在1911年出版了該定理。...
這組定理是數理統計學和誤差分析的理論基礎,指出了大量隨機變數累積分布函式逐點收斂到常態分配的積累分布函式的條件。中文名 中心極限定理 外文名 central limit ...
D,有當n→∞時,fn(x)→f(x),則函式f(x)稱為函式列{fn}(或{fn(x)})在D上的極限函式,這時也說,函式列{fn}在D上處處收斂於f,或在D上逐點收斂於f...
對一般的函式列來說,除研究它的逐點收斂(或稱點態收斂)這種收斂方式外,還要研究一致收斂,這是為了研究極限函式是否繼承相應函式列的各項(函式)所具有的分析性質(...
第14章 一致收斂 28714.1 函式的極限值 28714.2 逐點收斂與一致收斂 29014.3 一致收斂性與連續性 29414.4 一致收斂的度量 29614.5 函式級數和WeierstrassM...
(連續函式的對應命題需要比逐點收斂更強的條件,例如一致收斂。)(5)只有可測函式可以進行勒貝格積分。(6)一個勒貝格可測函式是一個實函式f:R→R,使得對於每一...
.2 )函式序列 { fn}在 [a,b]上逐點收斂於一連續函式 f :[a,b]→ R ,那么函式序列 { fn}在 [a,b]上一致收斂於函式....
布爾代數 A 的斯通氏空間是在 A 上的所有二值同態的集合,帶有這種同態的網逐點收斂的拓撲。(構造 A 的斯通氏空間的可替代和等價的方式是作為 ...
由於泛函分析源自研究各種函式空間,在函式空間裡函式列的收斂有不同的類型(譬如逐點收斂,一致收斂,弱收斂等等),這說明函式空間裡有不同的拓撲。而函式空間一般是...
34 存在某個拓撲空間X, X的點都是函式, 其拓撲相當於逐點收斂, 而X不是可度量化的空間35 存在某個函式序列 fn , 其圖像序列 G fn 收斂, 但 fn 並不...
布爾代數 A 的斯通氏空間是在 A 上的所有二值同態的集合,帶有這種同態的網逐點收斂的拓撲。(構造 A 的斯通氏空間的可替代和等價的方式是作為 ...
4.3.3 傅立葉級數的逐點收斂定理4.3.4 任意有限區間上的傅立葉級數4.3.5 傅立葉級數的逐項求權與逐項求導數4.3.6 傅立葉級數的極值性質與貝塞爾不等式習題...
