以機率1收斂(converges with probability one)亦稱幾乎必然收斂.、幾乎處處收斂、幾乎肯定收斂,是隨機變數列的一種較強的收斂性。若隨機變數列以機率1收斂,則它必然依機率收斂,反之則未必。
基本介紹
- 中文名:以機率1收斂
- 外文名:converges with probability one
- 別名:幾乎必然收斂、幾乎處處收斂等
- 所屬領域:機率論
- 相關概念:隨機變數列、依機率收斂等
定義
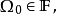
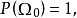





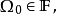
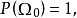

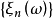
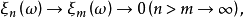

以機率1收斂的判別準則
定理

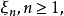
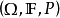

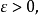
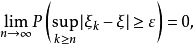
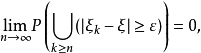
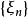
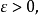
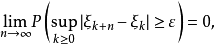

定理證明
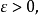

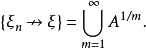
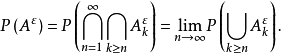

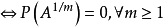
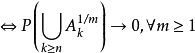
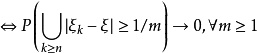
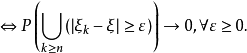
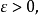
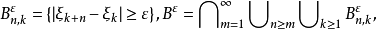

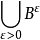
推論
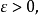


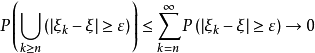

以機率1收斂(converges with probability one)亦稱幾乎必然收斂.、幾乎處處收斂、幾乎肯定收斂,是隨機變數列的一種較強的收斂性。若隨機變數列以機率1收斂,則它必然依機率收斂,反之則未必。
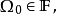
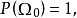





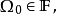
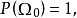

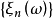
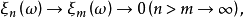


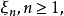
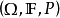

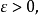
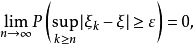
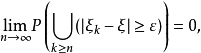
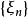
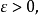
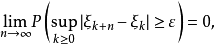

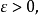

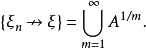
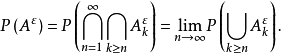

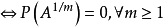
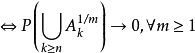
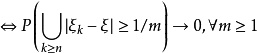
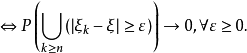
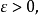
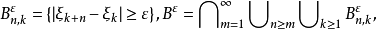

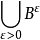
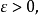


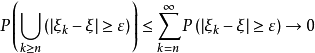
以機率1收斂(converges with probability one)亦稱幾乎必然收斂.、幾乎處處收斂、幾乎肯定收斂,是隨機變數列的一種較強的收斂性。若隨機變數列以機率1收斂,則它必然...
機率收斂性(convergence in probability)是隨機圖的性質,指一種在機率意義下的收斂性。...
機率論中的極限定理和數理統計學中各種統計量的極限性質,都是按隨機變數序列的各種不同的收斂性來研究的。...
依機率收斂,convergence in probability,別稱隨機收斂,套用於機率論與數理統計。...... 依機率收斂,convergence in probability,別稱隨機收斂,套用於機率論與數理統計。...
函式列的收斂性到隨機變數列的推廣。與函式列的收斂性不同,隨機變數列的收斂性是在慨率意義下的收斂性。最常用的是:依分布收斂、依機率收斂,以機率1收斂和r階...
亦稱“隨機收斂”。稱隨機變數列{Xn}依機率收斂於隨機變數X, 記作 或 ,如果對於任意 ,有 。 [2] 收斂性以機率1收斂 亦稱幾乎必然收斂。稱隨機變數列X1,X2...
均方收斂(convergence in the mean square指的是機率論中常用的一種收斂性。...... 均方收斂(convergence in the mean square指的是機率論中常用的一種收斂性。...
通過隨機變數序列與其極限之差r階矩可以任意小來描述的收斂性,設r>0為常數,...對於某個r>0,有 E|ξ𝚗-ξ|ʳ<∞,則ξ𝚗以機率1收斂於ξ。[2] ...
依分布收斂是隨機變數列的一種收斂性,設{ξn,n≥1}是機率空間(Ω,F,P)上的隨機變數列,其相應的分布函式列為{Fn(x),n≥1},如果Fn(x)弱收斂於隨機變數...
強大數定律可能是機率論中最廣為人知的結果,它表明了獨立同分布的隨機變數序列的均值以機率1收斂到分布的均值 [1] 。定理1 [強大數定律]設 為一獨立同分布的...
如果中只含機率為1或為0的事件,則稱過程X為遍歷的,這時以機率1收斂於EX(0)=EX(t)。後一結果也稱為嚴平穩過程的強大數律,它表明,過程幾乎所有的樣本對時間...
柯爾莫哥洛夫強大數律(Kolmogorov strong law of large numbers)是最重要最常用的強大數律。若{Xn}為獨立同分布隨機變數序列,EXn存在,則以機率1成立n個獨立同...
強一致性(strong consistency)參數估計的一種收斂性質.指參數估計值以機率為1收斂到參數真值.又稱為強相容性.設丫一(y}l)}y}2),...}y(n>為R”中一隨機...
機率論歷史上第一個極限定理屬於伯努利,後人稱之為“大數定律”。機率論中討論隨機變數序列的算術平均值向隨機變數各數學期望的算術平均值收斂的定律。在隨機事件的...
關於隨機變數列在一定收斂意義下收斂於某隨機變數的定理的總稱,包括大數定律、小數定律、中心極限定理、局部極限定理等。隨機變數、分布函式列(機率分布列、特徵函式...
模擬退火算法與初始值無關,算法求得的解與初始解狀態S(是算法疊代的起點)無關;模擬退火算法具有漸近收斂性,已在理論上被證明是一種以機率收斂於全局最優解的...
,在此樣本空間上導出的機率分布序列記為{}。將分布函式序列{}的弱收斂概念加以推廣,可以研究序列{}的弱收斂問題,也可以研究過程樣本函式列以機率1收斂的問題,...
