基本介紹
- 中文名:依分布收斂
- 外文名:convergence in distribution
- 所屬學科:數學
- 相關概念:隨機變數序列、依機率收斂等
定義
定義1



定義2


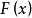

實例分析


















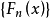
相關定理
定理1

定理2





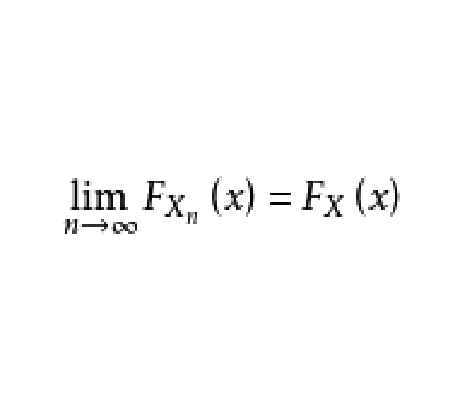





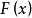



















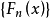






依分布收斂是隨機變數列的一種收斂性,設{ξn,n≥1}是機率空間(Ω,F,P)上的隨機變數列,其相應的分布函式列為{Fn(x),n≥1},如果Fn(x)弱收斂於隨機變數...
依機率收斂,convergence in probability,別稱隨機收斂,套用於機率論與數理統計。...... 依機率收斂是一種常見的收斂性質。依機率收斂比依分布收斂更強,比平均收斂則要...
收斂性依分布收斂 亦稱“弱收斂”,稱隨機變數列依分布收斂於隨機變數X,記作Xn⇒X,如果在X的分布函式 F(x)的每一連續點x上,Xn的分布函式Fn(x)收斂於F(x)...
設、分別表示隨機變數、的分布函式,若對的每一個連續點都有 機率論中的收斂 ,則稱的分布弱收斂於的分布,也稱依分布收斂於。分布弱收斂還有各種等價條件,例如,對...
機率收斂性是隨機圖的性質,指一種在機率意義下的收斂性。隨機圖的一些性質可以看作隨機變數,對於隨機變數Xn,若對任意ε>0,滿足 則稱Xn依機率收斂於l。這種收斂...
是獨立同分布隨機變數序列,期望為 ,則 收斂到u。如果說“弱大數定律”,上述收斂是指依機率收斂(in probability),如果說“強大數定律”,上述收斂是指幾乎必然收斂...
2.2 隨機變數的函式的分布2.3 多元正態分布2.4 一個重要的例子:正態分布中的抽樣分布2.5 習題第3章 各種收斂方式與極限分布3.1 依機率收斂...
依分布收斂於標準常態分配N(0,1)。基於這個性質可知, 當n較大時,可用作為μ 的區間估計,其中是標準常態分配的上分位數(見機率分布);這個估計的置信係數當n...
這時,也稱隨機過程式列{,≥1}依分布收斂到,記作 隨機過程的極限定理 同樣,這一結果之所以稱為(弱)不變原理,是因為極限分布不依賴原序列{ξ,≥1}的公共分布。...
例如,設x1,x2,…,xn為抽自參數為p的二點分布(見機率分布)的樣本,當n→∞時,依分布收斂(見機率論中的收斂)於標準常態分配N(0,1),以 uα/2記N (0,...
(θ)為待估函式,記 式中稱為費希爾信息量,若g(θ)的估計量為抭n(X1、X2…Xn),當n→時,依分布收斂於常態分配 N(0,v2(θ)),就稱此估計量為g(θ)...
7.2.2收斂定理 .1247.3隨機級數的收斂 1297.4重對數律 .132第8章中心極限定理 .1338.1測度的弱收斂、隨機變數的依分布收斂 .133...
隨機測度的收斂與極限問題相應於測度序列的各種收斂性,可以定義隨機測度(隨機點過程)的弱收斂、強收斂、淡收斂、依分布收斂等(見機率論中的收斂),並可研究其相互...
例如,設x1,x2,…,xn為抽自參數為p的二點分布的樣本,當n→∞時,依分布收斂(見機率論中的收斂)於標準常態分配N(0,1),以 uα/2記N (0,1)的上 α/...
