弱收斂(weakly convergence)是一種收斂性,有點列的弱收斂、運算元列的弱收斂和泛函列的弱收斂三種情況。
基本介紹
- 中文名:弱收斂
- 外文名:weakly convergence
- 分類:點列、運算元列、泛函列的弱收斂
- 性質:強收斂一定弱收斂
- 領域:泛函分析
- 學科:數學
點列
點列的弱收斂

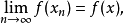

性質
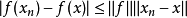



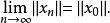
運算元列
運算元列的弱收斂
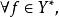

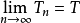



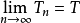
性質
泛函列
泛函列的弱收斂



性質

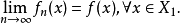
弱收斂(weakly convergence)是一種收斂性,有點列的弱收斂、運算元列的弱收斂和泛函列的弱收斂三種情況。

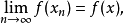

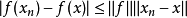



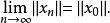
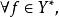

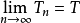



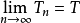




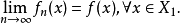
弱收斂(weakly convergence)是一種收斂性,有點列的弱收斂、運算元列的弱收斂和泛函列的弱收斂三種情況。...
淡收斂(vague convergence)是機率測度的一種收斂性。由奧地利數學家黑利(Helly,E.)選擇定理的推廣知,(R,B)上任一機率測度序列都有淡收斂的子序列。...
機率論中的極限定理和數理統計學中各種統計量的極限性質,都是按隨機變數序列的各種不同的收斂性來研究的。...
弱∗收斂(weak ∗ convergence)是一種收斂性,指依弱∗拓撲收斂。...... 弱收斂是一種收斂性,有點列的弱收斂、運算元列的弱收斂和泛函列的弱收斂三種情況。...
記測度全體為M,對任何具緊支集的連續實函式f,網(列){∫fdμi}收斂於∫fdμ,稱M中的網(列)(μi)i∈I渾收斂於μ∈M。...
弱序列完備(weak sequential completeness )是關於弱拓撲的序列完備性。設X是賦范線性空間,X*是X的共軛空間,稱X(X*)是弱(弱*)序列完備,是指X(X*)中的任何...
點列(range of points)是射影幾何的基本概念之一,指一條直線上所有點的集合。該直線稱為點列的底。收斂點列一定是基本點列,但基本點列不一定有極限。由點...
弱收斂於某分布函式F(x)的充分和必要條件是,相應的特徵函式列φ1(t),φ2(t)二收斂於某連續函式φ(t)。這時,φ(t)就是分布函式F(x)的特徵函式,而且φn...
渾拓撲(vague topology)是一種特殊拓撲,在M(X)上用渾收斂定義的拓撲稱為渾拓撲。...... 當核K為α核時,測度網(列)強收斂必弱收斂,弱收斂必渾收斂。...
若巴拿赫空間X有巴拿赫-薩克斯性質,則它必有弱巴拿赫-薩克斯性質。...... 若X中每個弱收斂的點列{xn}有一子列 ,使它的算術平均值按範數收斂於X中的一個元x0...
《現代數學基礎:泛函分析中的反例》匯集了泛函分析中的大量反例,主要內容有度量空間、賦范線性空間、線性運算元、弱拓撲和弱*拓撲、向量值函式、不動點理論、Hilbert...
弱列緊是與弱收斂相聯繫的列緊性。弱(弱∗)列緊以及弱(弱∗)收斂、弱(弱∗)序列完備等都是賦范線性空間理論中的重要概念。...
設X是巴拿赫空間,若X*中的點列{fn}弱收斂等價於{fn}弱∗收斂,則x稱為格羅騰迪克-巴拿赫空間,簡稱G-B空間。...
主要內容有:距離空間、一般向量空間、Banach空間和F空間、線性運算元、線性泛函與線性泛函方程、雙正交序列與弱收斂序列、等距與同構理論、線性維數,以及Banach空間現代...
,則稱 弱收斂於 ,記為 ),並稱相應的運算元 為弱無窮小運算元。無窮小運算元A是線性的,但未必有界 [1] 。無窮小運算元馬爾可夫過程的無窮小運算元 編輯 無窮...
弱運算元拓撲(weak operator topology)是運算元空間中的一種局部凸拓撲。...... 弱運算元拓撲是運算元空間中的一種局部凸拓撲。...運算元定向列{Aα}弱收斂於運算元A,記為 ...
弱可測矢量值函式是可測數值函式概念在賦范線性空間上的另一種重要的推廣。...... 弱可測函式列關於μ幾乎處處弱收斂的極限是弱可測的。弱可測矢量值函式弱可...
將分布函式序列{}的弱收斂概念加以推廣,可以研究序列{}的弱收斂問題,也可以研究過程樣本函式列以機率1收斂的問題,後者有時也稱為強收斂問題。 機率測度弱收斂 用...
依機率或以機率1收斂於零,則分別稱 是依機率穩定或以機率1穩定的。這是大數律的一種推廣形式。由於 依機率收斂於零與 的分布向集中於零的退化分布弱收斂是等價...
強列緊是與強收斂相聯繫的列緊性。設X是賦范線性空間,S是X的子集,如果S中任何點列都有強收斂(即按範數收斂)的子列,則稱S是強列緊的。...
《測度論講義》,科學出版社2004年出版的圖書,作者是嚴加安。《測度論講義》系統介紹一般可測空間和Hausdorff空間上的測度與積分、測度的弱收斂和淡收斂,以及與測度論...
