機率論中的極限定理和數理統計學中各種統計量的極限性質,都是按隨機變數序列的各種不同的收斂性來研究的。
基本介紹
- 中文名:機率論收斂
- 外文名:Convergence of probability theory
- 套用學科:高等數學
- 適用領域範圍:航天、金融、計算機
- 適用領域範圍:統計學
- 拼 音:gàilǜlùnshōuliǎn
設{,≥1}是機率空間(,F,)(見機率)上的隨機變數序列,從隨機變數作為可測函式看,常用的收斂概念有以下幾種:
若,則稱{,≥1}以機率1收斂於。強大數律(見大數律)就是闡明事件發生的頻率和樣本觀測值的算術平均分別以機率 1收斂於該事件的機率和總體的均值。以機率 1收斂也常稱為幾乎必然(簡記為.)收斂,它相當於測度論中的幾乎處處(簡記為..)收斂。
若對任一正數ε,都有,則稱{,≥1}依機率收斂於。它表明隨機變數與發生較大偏差(≥ε)的機率隨無限增大而趨於零。機率論中的伯努利大數律就是最早闡明隨機試驗中某事件發生的頻率依機率收斂於其機率()的。依機率收斂相當於測度論中的依測度收斂。
對≥1,若-的階絕對矩(見矩)的極限,則稱{,≥1}階平均收斂於。特別,當=1時,稱為平均收斂;當=2時,稱為均方收斂,它在寬平穩過程(見平穩過程)理論中是一個常用的概念。
設的均值都是有限的,若對任一有界隨機變數都有,則稱{,≥1}弱收斂於。由平均收斂可以推出弱收斂。
從隨機變數的分布函式(見機率分布)看,常用的有如下收斂概念。
設、分別表示隨機變數、的分布函式,若對的每一個連續點都有,則稱的分布弱收斂於的分布,也稱依分布收斂於。分布弱收斂還有各種等價條件,例如,對任一有界連續函式(),
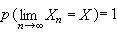 機率論中的收斂
機率論中的收斂 機率論中的收斂
機率論中的收斂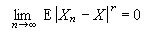 機率論中的收斂
機率論中的收斂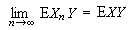 機率論中的收斂
機率論中的收斂 機率論中的收斂
機率論中的收斂設{(),≥1}為分布函式列,而()為一非降右連續函式(不一定是分布函式),若對()的每一個連續點都有,則稱淡收斂於。
上述各種收斂之間有如下蘊含關係(崊表示由可推出),若′≥≥1,則有:。此外,依機率收斂於常數與依分布收斂於常數是等價的。當是獨立隨機變數序列{,≥1}的部分和時,依分布收斂、依機率收斂和以機率1收斂三者是等價的。
隨著機率論的發展,上述收斂概念還推廣到取值於一般可測空間(見測度論)的隨機元(見隨機過程)序列的各種收斂性。例如隨機過程式列的分布弱收斂(見隨機過程的極限定理),巴拿赫空間隨機元序列的收斂等。
 機率論中的收斂
機率論中的收斂 機率論中的收斂
機率論中的收斂 機率論中的收斂
機率論中的收斂