基本介紹
- 中文名：伯恩斯坦多項式
- 外文名：Bernstein polynomial
- 領域：數值分析
- 命名來源：謝爾蓋納諾維奇伯恩斯坦
- 變形：貝塞爾曲線形式
- 發現時間：1912年
人物簡介,偏微分方程,機率論,近似理論,貝塞爾曲線,詳細定義,常用性質,
人物簡介
不定積分是由Sergei Natanovich Bernstein（俄羅斯語：СергейНатановичБернштейн，有時被羅馬化為伯恩斯坦; 1880年3月5日至1968年10月26日）提出的，他是俄羅斯和蘇聯猶太裔數學家，專研偏微分方程，微分幾何， 機率論和近似理論。
伯恩斯坦的主要成果有：
偏微分方程
機率論
1917年，伯恩斯坦提出了基於代數結構的第一個機率論的公理基礎。它隨後被Kolmogorov的測量理論方法所取代。
在20世紀20年代，他引入了一種用於證明相關隨機變數的和的極限定理的方法。
近似理論
通過套用伯恩斯坦多項式，他奠定了建構性功能理論的基礎，一個研究函式的平滑性與其多項式的近似關係的領域。特別地，他證明了Weierstrass近似定理和伯恩斯坦定理（近似理論）。
貝塞爾曲線
貝塞爾曲線(Bézier curve)，又稱貝茲曲線或貝濟埃曲線，是套用於二維圖形應用程式的數學曲線。一般的矢量圖形軟體通過它來精確畫出曲線，貝茲曲線由線段與節點組成，節點是可拖動的支點，線段像可伸縮的皮筋，我們在繪圖工具上看到的鋼筆工具就是來做這種矢量曲線的。貝塞爾曲線是計算機圖形學中相當重要的參數曲線，在一些比較成熟的點陣圖軟體中也有貝塞爾曲線工具，如PhotoShop等。在Flash4中還沒有完整的曲線工具，而在Flash5裡面已經提供出貝塞爾曲線工具。
貝塞爾曲線於1962，由法國工程師皮埃爾·貝塞爾（Pierre Bézier）所廣泛發表，他運用貝塞爾曲線來為汽車的主體進行設計。貝塞爾曲線最初由Paul de Casteljau於1959年運用de Casteljau演算法開發，以穩定數值的方法求出貝茲曲線。
詳細定義
伯恩斯坦多項式(Bernstein polynomial)逼近連續函式的一系列多項式。可在外爾斯特拉斯逼近定理的構造性證明中使用。設函式f：[0，1]→R(或C)，對於n∈N+，
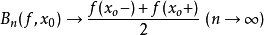
常用性質
伯恩斯坦多項式具有如下性質：
性質1：若v<0或v>n，則
。
性質2：對x∈[0，1]有
。
性質3：
在x=0處有一個v重根。
性質4：
在x=1處一個(n-v)重根。
性質5：無限積分由下式給出：
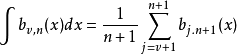
性質6：對給定的n來說有限積分是常數：
