基本介紹
- 中文名:斯通逼近定理
- 外文名:Stone's approximation theorem
- 適用範圍:數理科學
簡介,條件,具體內容,外爾斯特拉斯定理,
簡介
斯通逼近定理是外爾斯特拉斯定理的一個重要推廣。
條件
記C(X)為緊的豪斯多夫拓撲空間X上的連續函式的全體。若以自然的方式對C(X)中的元素f和g定義乘法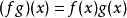 ,則C(X)成為一個代數。所謂代數就是一個線性空間,其中定義了元素之間的乘法,此乘法滿足如下的公設:
,則C(X)成為一個代數。所謂代數就是一個線性空間,其中定義了元素之間的乘法,此乘法滿足如下的公設:
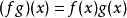
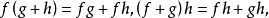

具體內容
作為外爾斯特拉斯定理的推廣,1937年,斯通(Stone,M.H.)建立了這樣的逼近定理:C(X)的任何子代數A在C(X)中稠密,只要它具有兩個性質:
1、1∈A;
2、A分離X中的點,即對X中任意兩個相異的點x和y,都有f∈A使得f(x)≠f(y)。
