外爾斯特拉斯－斯通定理是函式逼近論中的基本定理。外爾斯特拉斯定理是關於實變函式逼近的定理，它本身包含兩個結論：外爾斯特拉斯第一定理和外爾斯特拉斯第二定理。它們是相互獨立的，但又有聯繫，都是1885年由K.外爾斯特拉斯所得到的。
正文,
正文
函式逼近論中的基本定理。外爾斯特拉斯定理是關於實變函式逼近的定理，它本身包含兩個結論：外爾斯特拉斯第一定理和外爾斯特拉斯第二定理。它們是相互獨立的，但又有聯繫，都是1885年由K.外爾斯特拉斯所得到的。斯通定理是外爾斯特拉斯定理在抽象空間中的推廣。這個定理還可以推廣到用抽象元素的線性組合及其乘積來實現逼近。由斯通定理可以得到很多具體的逼近定理。 外爾斯特拉斯第一定理 對於任意一個在閉區間【,)】上的連續函式()，存在多項式序列{()}，它在【,)】上一致收斂到()。 外爾斯特拉斯第二定理 對於任意一個在實軸上以2π為周期的連續函式(),存在三角多項式序列{()}，它在實軸上一致收斂到()。 這兩個定理中的多項式序列 {()}和三角多項式序列{()}都是可以直接構造出來的。這樣一來,較為複雜的函式（如連續函式）就可以在所討論的區間上用較為簡單的函式（如多項式或三角多項式）近似地表達出來了，這在實用上就提供了很大的方便。進一步還可以研究多項式序列{()}(或三角多項式序列{()})趨向於()（或()）的速度，這就是最佳逼近值的階的估計。人們還研究其他函式系（如有理函式、廣義多項式、分段多項式等）的逼近問題。這些結果在空間中也成立，其中0<<+∞。 斯通定理 1937年，斯通在抽象空間中研究了逼近定理。設是某個度量空間中的集合,它至少含有兩個不同的元素，且成立有限覆蓋定理（或是緊的豪斯多夫拓撲空間）。設是上的連續函式集合，它構成線性空間且是環。此外，還具有性質：對於中任意兩個不同的元素,,在中存在函式(),使()≠(),則對於上的任意連續函式(),在中存在函式序列{()}，它在上一致收斂到()。 由斯通定理，可以推出多維空間中的外爾斯特拉斯定理，以及在實軸上用有理函式來逼近在實軸上連續且存在的函式()的定理等。 這些定理在複平面上還有各種推廣。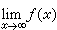
外爾斯特拉斯－斯通定理
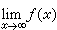外爾斯特拉斯－斯通定理