基本介紹
- 中文名:區間套定理
- 外文名:theorem of nested interval
- 別稱:閉區間套定理
- 套用學科:數學
- 適用領域範圍:實數的完備性
- 屬性:實數集完備性的基本定理
定義,定理(閉區間套定理),性質,推論,注,套用領域,
定義
設閉區間列 具有如下性質:
具有如下性質:

(i)

(ii)

則稱 為閉區間套,或簡稱區間套。
為閉區間套,或簡稱區間套。

這裡性質(i)表明,構成區間套的閉區間列是前一個套著後一個,即各閉區間的端點滿足如下不等式:

定理(閉區間套定理)
若 是一個區間套,則在實數系中存在惟一的一點
是一個區間套,則在實數系中存在惟一的一點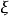 ,使得
,使得 ,即
,即

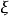


證 由(1)式,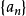 為遞增有界數列,依單調有界定理,
為遞增有界數列,依單調有界定理,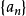 有極限
有極限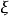 ,且有
,且有
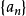
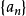
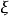




最後證明滿足(2)的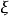 是惟一的,設數
是惟一的,設數 也滿足
也滿足
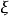



由區間套的條件(ii)得


性質
由(4)式容易推得如下很有用的區間套性質。
推論
若 是區間套
是區間套 所確定的點,則對任給的
所確定的點,則對任給的 ,存在
,存在 ,使得當
,使得當 時有
時有






注
區間套定理中要求各個區間都是閉區間,才能保證定理的結論是成立的。對於開區間列,如 ,雖然其中各個開區間也是前一個包含後一個,且
,雖然其中各個開區間也是前一個包含後一個,且 ,但不存在屬於所有開區間的公共點。
,但不存在屬於所有開區間的公共點。


套用領域
例 用區間套定理證明連續函式根的存在性定理。
證 設 在區間
在區間 上連續,
上連續, ,並且記
,並且記 。令
。令 ,如果
,如果 ,結論已經成立。若
,結論已經成立。若 ,那么
,那么 與
與 有一個小於零,不妨設
有一個小於零,不妨設 ,記
,記 。再令
。再令 ,如果
,如果 ,結論已經成立。故同樣可設
,結論已經成立。故同樣可設 。那么
。那么 在
在 與
與 這兩個區間中的某一個區間上端點值異號,並記這個區間為
這兩個區間中的某一個區間上端點值異號,並記這個區間為 。將這個過程無限重複下去,就得到一列閉區間
。將這個過程無限重複下去,就得到一列閉區間 ,滿足
,滿足



















(1)

(2)

(3)

由(1)和(2)可知 是一個區間套,由區間套定理,存在
是一個區間套,由區間套定理,存在 ,且有
,且有 。因為
。因為 在點
在點 連續,所以由(3)得
連續,所以由(3)得









