基本介紹
- 中文名:區間套qujian
- 外文名:nest of intervals
- 所屬學科:數學
- 相關定理:區間套定理、矩形套定理等
定義


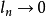
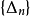
區間套定理
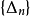





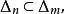


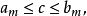

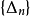

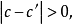

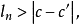

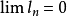
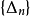





詳細介紹
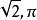


 圖1 區間套序列
圖1 區間套序列






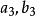








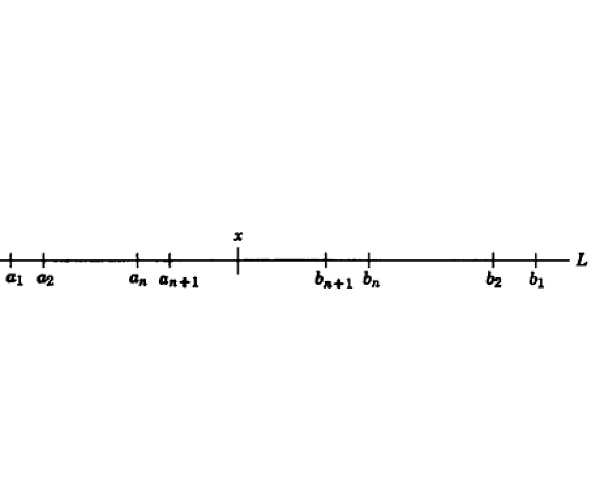


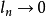
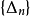
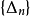





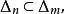


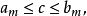

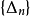

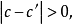

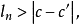

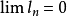
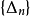





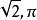


 圖1 區間套序列
圖1 區間套序列






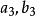








設在實軸上,有一組閉區間I1,I2,I3,…,In,…具有下述二種性質:(1)In+1全部在In中(n=1,2,3,…);(2)當n→∞時,區間In的長度趨向於0,則稱這組...
閉區間套定理:如果{[an,bn]}形成一個閉區間套,則在實數系中存在唯一的實數ξ屬於所有的閉區間[an,bn],n=1,2,3,…;即an≤ξ≤bn , n=1,2,3,…。...
閉區間是數學用語,與開區間相對。 閉區間是直線上的連通的閉集,是直線上介於固定兩點間的所有點的集合(包括給定的兩點),用[a,b]來表示(包含兩個端點a和b)(...
半開半閉區間(Semi open closed interval)是高中數學中函式的一種定義域,常簡稱為“半開區間”或“半閉區間”。半開半閉區間用“( ]”表示。半開半閉區間與...
區間套定理與單調有界定理、數列的緻密性定理和柯西收斂準則、聚點定理、有限覆蓋定理共同構成實數集完備性的基本定理,並且這六個定理是相互等價的,對於研究實數集的...
閉球套定理(closed ball nest theorem)對度量空間的完備性的一種刻畫。 歐氏空間中許多結論均依賴於空間的完備性,如直線上的閉區間套定理,平面內的閉矩形套定理...
上述用閉域套定理對有界閉域上二元連續函式的有界性定理進行證明,從一側面反映了此證明與用閉區間套定理證明閉區間上連續函式的有界性定理有異曲同工之妙,但...
但這裡有一個很微妙的問題,即與完備性公理等價的7個實數系的基本定理(確界存在定理、單調有界定理、有限覆蓋定理、聚點定理、緻密性定理、閉區間套定理和柯西收斂...
實數連續性定理包括:確界存在性定理,單調有界收斂定理,閉區間套定理,有限覆蓋定理,聚點定理,波爾查諾——魏爾斯特拉斯定理、柯西準則。 這七個定理可由確界存在...
