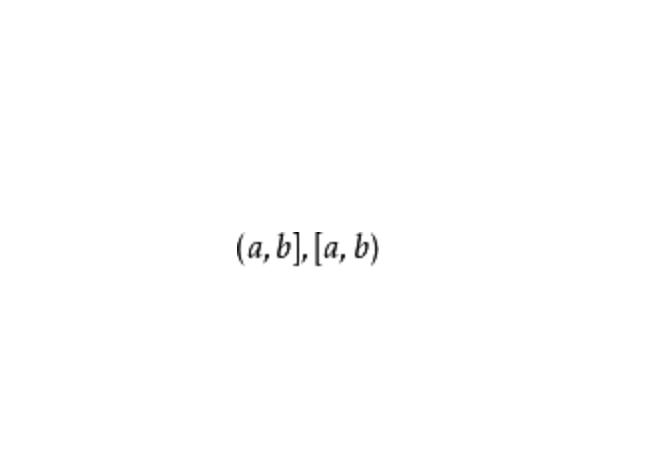半開半閉區間（Semi open closed interval）是高中數學中函式的一種定義域，常簡稱為“半開區間”或“半閉區間”。半開半閉區間用“（ ]”表示。半開半閉區間與區間的其他兩種（開區間和閉區間）又稱為有界區間或有限區間，其他的稱為無界區間或無限區間。
基本介紹
- 中文名：半開半閉區間
- 外文名：Semi open closed interval
- 簡稱：半開區間或半閉區間
- 類型：數軸上一種常用的點集
- 一級學科：數學
- 二級學科：實數理論
簡介（區分開區間、閉區間）,定義,概念拓展（鄰域）,鄰域公理,開鄰域和閉鄰域,重要結論,
簡介（區分開區間、閉區間）
區間（interval）是數軸上一種最常用的點集。它有三類：閉區間[a,b]={x|a≤x≤b}，其中a,b是實數（下同）；開區間(a,b)={x|a<x<b}，(a,+∞)={x|x>a}，(-∞,b)={x|x<b}，(-∞,+∞)=R；半開半閉區間(a,b]={x|a<x≤b}，[a,b)={x|a≤x<b}，[a,+∞)={x|x≥a}，(-∞,b]={x|x≤b}。
半開半閉區間也稱作“半開區間”或“半閉區間”。上面區間的a,b分別稱為相應的區間的左、右端點，區間中其他點稱為該區間的內點。上述各種區間中，[a,b]，(a,b)，[a,b)，(a,b]又稱有界區間或有限區間，其他的稱為無界區間或無限區間。
對於a>0，區間[-a,a]，(-a,a)又稱為對稱區間。區間是數軸上的線段或射線或整個數軸，“開”（”閉“，”半開“）是指不包含（包含，只包含一個）其端點。在擴張的實數系R*中，四種開區間可以用一個記號(a,b)表示，其中-∞≤a<b≤+∞。類似地，半開區間可以用[a,b)(a∈R，b∈R*)或(a,b](a∈R*，b∈R)表示。b-a稱為區間的長度。無界區間的長度是+∞。R*本身也可寫作[+∞,-∞]。除了單點集外，區間是R中僅有的連通集。文獻中常有以”]“和”[“分別代替”(“和”)“，而把(a,b)寫作 ]a,b[ 的寫法，類似地也有 ]a,-∞[ 等寫法。
定義
設a和b是兩個不同的實數，且a<b，
滿足不等式a<X<b的所有實數X所組成的集合叫開區間，用記號（a，b）表示；
滿足不等式a≤X≤b的所有實數X所組成的集合叫閉區間，用記號[a,b] 表示；
滿足不等式a≤X<b或a<X≤b的所有實數X所組成的集合叫半開半閉區間，分別表示為[a,b),(a,b]。
概念拓展（鄰域）
鄰域公理
給定集合X，映射U：X→P(P(X))（其中P(P(X))是X的冪集的冪集），U將X中的點x映射到X的子集族U(x)），稱U(x)是X的鄰域系以及U(x)中的元素（即X的子集）為點x的鄰域，若且唯若U滿足以下的鄰域公理：
- U1：若集合A∈U(x)，則x∈A。
- U2：若集合A，B∈U(x)，則A∩B∈U(x)。
- U3：若集合A∈U(x)，且A ⊆ B ⊆ X，則B∈U(x)。
- U4：若集合A∈U(x)，則存在集合B∈U(x)，使B ⊆ A，且∀y∈B，B∈U(y)。
對鄰域公理的解釋：鄰域公理是現代數學拓撲結構的基礎概念，是定義拓撲的五套等價公理之一。這套公理直接定義了空間上的整套領域系，而非簡單定義某個點的鄰域。映射U即是將x映射至x鄰域組成的集合。
- U1的解釋：若A是x的鄰域，則x屬於A。這是顯然的。
- U2的解釋：若A和B都是x的鄰域，則A和B的交集也是x的鄰域。即鄰域對於有限交運算封閉。
- U3的解釋：若A是x的鄰域，則所有包含A的集合都是x的鄰域。
- U4的解釋：若A是x的鄰域，則存在一個被A包含的集合B（可以相等），使得B是其中所有點的鄰域。換言之，若x有一個鄰域，那么一定可以將其縮小，縮小到它是其中所有點的鄰域。更關鍵的，這樣的鄰域若且唯若它是X中的開集，這也是鄰域公理為何等價於開集公理，從而可以通過它定義X上拓撲的原因。
