基本介紹
定理
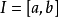
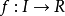


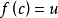



與完整性的關係

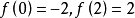


證明
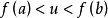
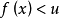
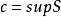
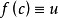
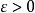
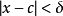
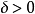
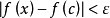









歷史
反介值定理是錯的
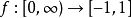
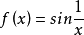
套用
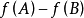
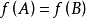
特殊情況
幾何意義
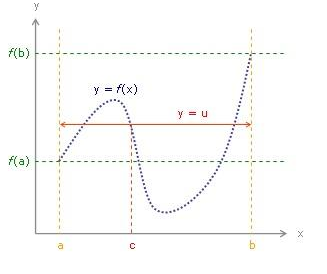
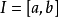
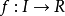


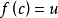




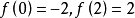


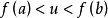
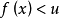
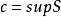
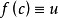
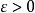
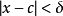
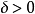
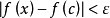









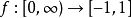
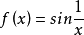
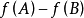
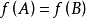

介值定理,又名中間值定理,是閉區間上連續函式的性質之一,閉區間連續函式的重要性質之一。在數學分析中,介值定理表明,如果定義域為[a,b]的連續函式f,也就是說...
積分中值定理,是一種數學定律。分為積分第一中值定理和積分第二中值定理,它們各包含兩個公式。其中,積分第二中值定理還包含三個常用的推論。積分中值定理揭示了...
由於連續函式介值定理有廣泛的套用,因此導函式介值定理(Darboux定理)與導函式商的介值定理(在不要求導函式連續的情況下)也有廣泛的套用。...
零值定理為介值定理的推論.又名零點定理.其內容為:設函式f(x)在閉區間[a,b]上連續,且f(a)與 f(b)異號(即f(a)× f(b)<0),那么在開區間(a,b)內...
假設函式f(x)在閉區間[a, b]上連續,且函式值f(a)與f(b)異號(即,一為正一為負)。則在開區間(a, b)上必定存在至少一個c,使得f(c) = 0。勘根定理...
微分中值定理是一系列中值定理總稱,是研究函式的有力工具,其中最重要的內容是拉格朗日定理,可以說其他中值定理都是拉格朗日中值定理的特殊情況或推廣。微分中值定理...
積分第一中值定理是積分中值定理的推廣之一,此外還有積分第二中值定理。積分中值定理揭示了一種將積分化為函式值, 或者是將複雜函式的積分化為簡單函式的積分的...
在極限理論中,我們知道閉區間上連續函式具有5個性質,即:有界性定理、最大值與最小值定理、介值定理、零點定理和一致連續性定理。其中,零點定理是介值定理的一個...
代數基本定理代數證明 這個證明需要依賴實數集的如下事實:正實數R在 上有實平方根,以及任何奇次多項式在 上有一個根(這可以用介值定理證明)。...
這個定理最早由伯納德·波爾扎諾證明,當他在證明介值定理時,附帶證明了這個定理,但是他的證明已經散佚。卡爾·魏爾施特拉斯獨自發現並證明了這個定理。波爾扎諾-魏...
數學定理列表(按字母順序排列) 以下列出了許多數學定理,供查閱與引用。...介值定理積分第一中值定理緊緻性定理積分第二中值定理夾逼定理卷積定理 極值定理...
1817年,緻密性定理作為證明介值定理的引理第一次被波爾查諾證明。過了50多年後,其等價命題——聚點定理被發現並由維爾斯特拉斯證明。自此以後,波爾查諾-維爾斯...
這個定理最早由伯納德·波爾扎諾證明,當他在證明介值定理時,附帶證明了這個定理,但是他的證明已經散佚。卡爾·魏爾施特拉斯獨自發現並證明了這個定理。波爾扎諾-魏...
10.了解連續函式的性質和初等函式的連續性,理解閉區間上連續函式的性質(有界性、最大值和最小值定理、介值定理),並會套用這些性質....
一、有界性與最大值最小值定理 習題5-3 二、零點定理與介值定理 第四節反常積分 *三、一致連續性 一、無窮限的反常積分 習題1-10 二、無界函式的反常積分...
有界閉區域D上的多元連續函式在D上一定存在最大值和最小值。閉區域介值定理 有界閉區域D上的多元連續函式必定能在D上取得介於它的最大值與最小值之間的任何...
