如果函式y= f(x)在區間[a,b]上的圖象是連續不斷的一條曲線,並且有f(a)·f(b)<0,那么,函式y= f(x)在區間(a,b)內有零點,即存在c∈(a,b),使得f(c)=0,這個c也就是方程f(x)= 0的根。
基本介紹
- 中文名:零點定理
- 套用學科:數學
- 適用領域範圍:函式
- 相關:閉區間套定理
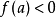
如果函式y= f(x)在區間[a,b]上的圖象是連續不斷的一條曲線,並且有f(a)·f(b)<0,那么,函式y= f(x)在區間(a,b)內有零點,即存在c∈(a,b),使得f(c)=0,這個c也就是方程f(x)= 0的根。
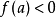
如果函式y= f(x)在區間[a,b]上的圖象是連續不斷的一條曲線,並且有f(a)·f(b)<0,那么,函式y= f(x)在區間(a,b)內有零點,即存在c∈(a,b),使得f...
(Hilbert's Nullstellensatz)[1] 設f_1,...,f_k是一組多項式. 方程組f_1=...=f_k=0無公共零點的充要條件是:存在另一組多項式a_1,...,a_k,使得...
《零點定理》是特瑞·吉列姆執導,克里斯托弗·瓦爾茲、梅蘭尼·蒂埃里、馬特·達蒙、盧卡斯·赫奇斯、本·威士肖主演的科幻片,於2013年12月19日在義大利上映。該片...
零值定理為介值定理的推論.又名零點定理.其內容為:設函式f(x)在閉區間[a,b]上連續,且f(a)與 f(b)異號(即f(a)× f(b)<0),那么在開區間(a,b)內...
設是定義在數域 k 上的函式, 我們把方程 f=0 在數域 k 中的解稱作f (在k中)的零點. 所有零點構成的集合稱作零點集。...
閉區間套定理:如果{[an,bn]}形成一個閉區間套,則在實數系中存在唯一的實數ξ屬於所有的閉區間[an,bn],n=1,2,3,…;即an≤ξ≤bn , n=1,2,3,…。...
在極限理論中,我們知道閉區間上連續函式具有5個性質,即:有界性定理、最大值與最小值定理、介值定理、零點定理和一致連續性定理。其中,零點定理是介值定理的一個...
介值定理,又名中間值定理,是閉區間上連續函式的性質之一,閉區間連續函式的重要性質之一。在數學分析中,介值定理表明,如果定義域為[a,b]的連續函式f,那么在...
書籍信息書名不動點與零點的疊代方法及其套用 書號978-7-118-10939-9 作者周海雲 出版時間2016年6月 譯者 版次1版1次 開本16 裝幀精裝 出版基金國防科技圖書...
2013 零點定理 赤焰戰場2 Frog 2014 萬物理論 Professor Sciama 2015 罪惡之家 The Inspector 2015 回到從前 肯尼斯雷恩斯教授 2017 神奇女俠 阿瑞斯 2017 ...
1.5 零點與理想1.6 希爾伯特零點定理第二章 多項式系統的零點分解2.1 三角系統2.2 基於特徵列的算法2.3 改良的賽登貝格算法2.4 基於子結式的算法...
一、有界性與最大值最小值定理 習題5-3 二、零點定理與介值定理 第四節反常積分 *三、一致連續性 一、無窮限的反常積分 習題1-10 二、無界函式的反常積分...
