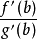設y=f(x)在(A,B)區間中可導，且[a,b]包含於(A,B)，f'(a)<f'(b)，則對於任意給定的η:f'(a)<η<f'(b),都存在一點c∈(a,b)使得f'(c)=η。
基本介紹
- 中文名：達布中值定理
- 數學表達形式：設y=f(x)在(A,B)區間中
- 其它表達形式：若函式f(x)在[a,b]上可導
- 達布中值定理：保持定號
表達形式,數學表達形式,等價形式,其它表達形式,證明,方法1,方法2,套用,
表達形式
數學表達形式
設y=f(x)在(A,B)區間中可導，且[a,b]包含於(A,B)，f'(a)<f'(b)，則對於任意給定的η:f'(a)<η<f'(b),都存在一點c∈(a,b)使得f'(c)=η。
等價形式
設f(x)在 [a,b]上可微，若在 [a,b]上f′(x)不等於0 ，則f′(x)在[a,b] 上保持定號(恆正或恆負)。
其它表達形式
若函式f(x)在[a,b]上可導，則f′(x)在[a,b]上可取f′(a)和f′(b)之間任何值。
證明
方法1
已知f'(a)<η<f'(b)，構造函式：g(x)=f(x)-ηx。
若g(a)=g(b)，則由羅爾中值定理：存在ε∈(a,b)使g'(ε)=0。
不妨設g(a)>g(b)，又g'(b)>0，由極限保號性，存在ξ∈（a,b）使g(ξ)<g(b)<g(a)。
由介值定理存在ζ∈(a,ξ)使g(ζ)=g(b)。
又由羅爾中值定理，存在δ∈(ζ,b)使g'(δ)=0。
所以無論如何總存在x∈(a,b)使g'(x)=0即f'(x)=η。
方法2
構造函式g(x)=f(x)-ηx。
由於f(x)在(a,b)區間內可導，所以f(x)在(a,b)區間內連續，故g(x)在(a,b)區間內連續。
補充定義使得g(x)在x=a，x=b處連續。
因為g'(a)=f'(a)-η<0,所以一定存在x>a,使得g(x)<g(a)，
即x=a不是函式g(x)在[a,b]上的最小值，同理x=b也不是函式g(x)在[a,b]上的最小值，
故g(x)在(a,b)區間內取得最小值，
所以必然存在ξ∈(a,b)，使g'(ξ)=f'(ξ)-η=0（費馬定理），
所以對於任意給定的η:f'(a)<η<f'(b),都存在一點c∈(a,b)使得f'(c)=η.
套用
由於連續函式介值定理有廣泛的套用，因此導函式介值定理(Darboux定理)與導函式商的介值定理(在不要求導函式連續的情況下)也有廣泛的套用。
我們知道平面曲線的最一般表示形式是參數形式。設曲線參數方程為
，x(t),y(t)在[a,b]上可導,且x′(t)在[a,b]上不為零,則在x′(t)與y(t)未必連續情況下，曲線切線的斜率可取兩端點切線斜率間任何值。事實上，曲線在任一點的切線斜率為
，由導函式商的介值定理 可取
與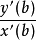
之間任何值。
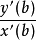
如果不用導函式商的介值定理，此結果很難證明。因為參數方程確定的曲線未必總能化為顯函式。即使能化為顯函式，就具體曲線而言，化成的顯函式的形式可能比較複雜，不利於研究它的性質。
此外,運用達布定理很容易看出：若函式f(x)在[a,b]上可導，則f′(x)在[a,b]上不可能存在第一類間斷點。
