基本介紹
- 中文名:羅爾中值定理
- 外文名:Rolle's theorem
- 別稱:羅爾定理
- 提出時間:1691年
- 套用學科:高等數學 微分學
- 適用領域範圍:物理、數學等
- 適用領域範圍:方程根的存在性
證明過程
幾何意義
幾種特殊情況


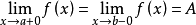









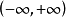

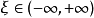


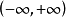
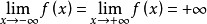

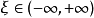


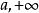




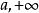





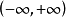

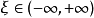


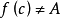

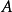







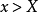


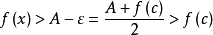

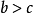





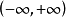
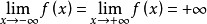
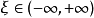



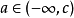




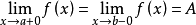









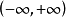

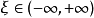


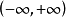
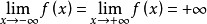

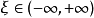


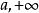




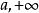





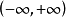

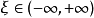


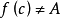

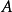







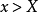


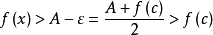

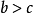





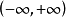
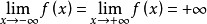
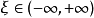



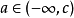

羅爾(Rolle)中值定理是微分學中一條重要的定理,是三大微分中值定理之一,其他兩個分別為:拉格朗日(Lagrange)中值定理、柯西(Cauchy)中值定理。羅爾定理描述如下:...
拉格朗日中值定理又稱拉氏定理,是微分學中的基本定理之一,它反映了可導函式在閉區間上的整體的平均變化率與區間內某點的局部變化率的關係。拉格朗日中值定理是羅...
達布中值定理方法1 已知f'(a)<η<f'(b),構造函式:g(x)=f(x)-ηx。若g(a)=g(b),則由羅爾中值定理:存在ε∈(a,b)使g'(ε)=0。...
微分中值定理主要包括羅爾定理、拉格朗日定理、柯西定理、泰勒定理,其中羅爾定理是拉格朗日定理等的預備定理,由三個已知條件推得結果,三個已知條件缺一不可,即若要...
拉格朗日定理存在於多個學科領域中,分別為:微積分中的拉格朗日中值定理;數論中的四平方和定理;群論中的拉格朗日定理 (群論)。...
拉格朗日中值定理是羅爾中值定理的推廣,同時也是柯西中值定理的特殊情形,是泰勒公式的弱形式(一階展開)。法國數學家拉格朗日於1797年在其著作《解析函式論》的第六...
一、羅爾中值定理 二、拉格朗日中值定理 三、柯西中值定理 四、泰勒中值定理 習題4—5 第六節洛必達法則 習題4—6 綜合題四 第五章導數與微分...
一、羅爾中值定理59二、拉格朗日中值定理60三、柯西中值定理61四、洛必達法則61習題一65第二節函式的單調性與極值65一、函式單調性的判別方法66二、函式的極值...
4.1.1 羅爾中值定理 4.1.2 拉格朗日中值定理 4.1.3 柯西中值定理 4.2 洛必達法則 4.2.1 00型不定式 4.2.2 其他不定式 4.3 函式的最值與極值 4.3.1 最值...
第三章 中值定理與導數的套用3.1 中值定理一、羅爾中值定理二、拉格朗日中值定理三、泰勒中值定理四、柯西中值定理習題3.13.2 洛必達法則...
3.5微分中值定理743.5.1羅爾中值定理743.5.2拉格朗日中值定理753.6洛必達法則763.6.100型和∞∞型763.6.2其他未定型783.7函式的單調性與函式的極值80...
4.1.1 羅爾中值定理4.1.2 拉格朗曰中值定理4.1.3 洛必達法則4.1.4 函式的單調性4.1.5 函式的極值4.1.6 函式的最大值和最小值...
第四章 導數的套用 48第一節 微分中值定理 48一、羅爾中值定理(Rolle) 48二、拉格朗日中值定理(Lagrange) 48習題4-1 50第二節 洛必達法則 50習題4-2 52...
第3章微分中值定理與導數的套用1033.1微分中值定理1033.1.1羅爾定理1033.1.2拉格朗日中值定理1053.1.3柯西中值定理108習題3 1110...
(1)了解羅爾中值定理、拉格朗日中值定理及它們的幾何意義。 (2)熟練掌握洛必達法則求“0/0”、“∞/ ∞”、“0·∞”、“∞-∞”、“1∞”、“00”和...
第3章微分中值定理與導數的套用1033.1微分中值定理1033.1.1羅爾定理1033.1.2拉格朗日中值定理1053.1.3柯西中值定理108習題3 1110...
什麼類型的題必須套用羅爾中值定理證明?證題的四個步驟和三種方法是什麼? 問題23 什麼類型的題套用拉格朗日中值定理證明?證題的兩種方法是什麼? 問題24 什...
《普通高等教育規劃教材:高等數學》的主要內容有:函式與極限、導數與微分、中值定理與導數的套用、不定積分、定積分及其套用、空間解析幾何與向量代數,多元函式微分...
5.6.1 羅爾中值定理的幾何意義 5.6.2 拉格朗日中值定理的幾何意義 5.7 泰勒公式與函式逼近 5.7.1 方便的Taylor函式 5.7.2 泰勒函式計算器 5.8 一...
第4章微分中值定理與導數的套用4.1微分中值定理4.1.1羅爾中值定理4.1.2拉格朗日中值定理4.1.3柯西中值定理習題4.14.2洛必達法則...
第一節拉格朗日中值定理及函式的單調性 一、羅爾中值定理 二、拉格朗日中值定理 三、函式的單調性 第二節 洛必達法則 一、洛必達法則 二、求未定式...
第3章 導數的套用3.1 微分中值定理3.1.1 拉格朗日中值定理3.1.2 羅爾中值定理3.1.3 柯西中值定理習題3.13.2 洛必達法則3.2.1 〓型或〓型的極限...
第三章微分中值定理與導數的套用99第一節微分中值定理99一、 羅爾中值定理99二、 拉格朗日中值定理101三、 柯西中值定理104習題3-1105...
第3章微分中值定理與導數的套用 3.1微分中值定理 3.1.1羅爾中值定理 3.1.2拉格朗日中值定理 3.1.3柯西中值定理 習題3.1 3.2洛必達法則 3.2.10...
