閉區間套定理:如果{[an,bn]}形成一個閉區間套,則在實數系中存在唯一的實數ξ屬於所有的閉區間[an,bn],n=1,2,3,…;即an≤ξ≤bn , n=1,2,3,…。且lim an=lim bn=ξ。
基本介紹
- 中文名:閉區間套定理
- 外文名:the principle of nested intervals
- 別稱:區間套原理
- 表達式:ξ∈{[an,bn]}
- 套用學科:數學
- 適用領域範圍:數學分析
定理定義
閉區間套
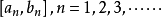
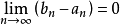
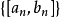
定理
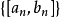
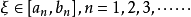
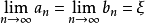
推論
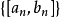

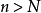
推導過程
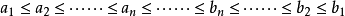
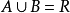

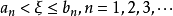
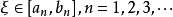
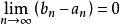
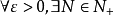
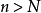
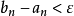
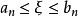
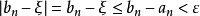
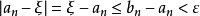
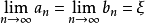
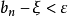
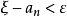
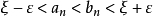
定律影響
單調有界定理
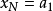
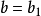
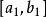
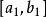
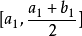
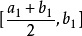
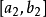
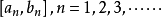
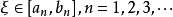
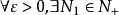
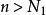
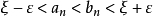
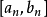
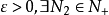
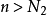
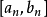
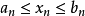

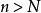
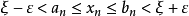
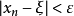
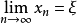
拉格朗日中值定理
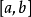


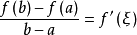
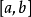


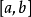
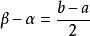
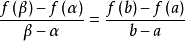
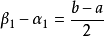
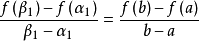
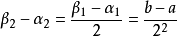
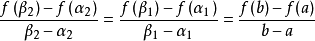
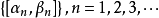

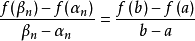
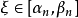
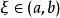
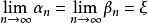
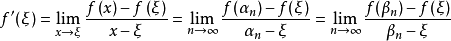
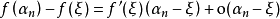
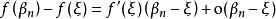
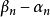
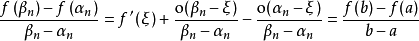
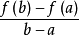
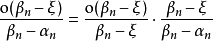
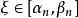

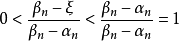
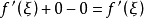
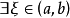
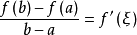
閉區間套定理:如果{[an,bn]}形成一個閉區間套,則在實數系中存在唯一的實數ξ屬於所有的閉區間[an,bn],n=1,2,3,…;即an≤ξ≤bn , n=1,2,3,…。且lim an=lim bn=ξ。
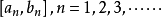
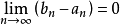
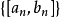
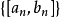
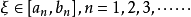
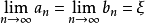
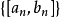

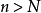
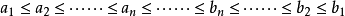
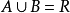

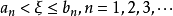
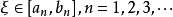
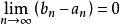
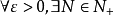
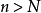
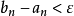
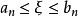
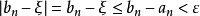
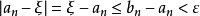
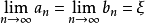
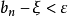
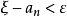
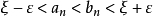
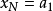
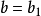
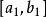
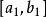
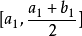
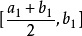
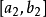
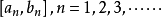
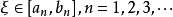
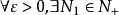
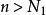
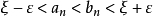
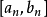
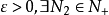
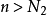
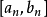
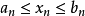

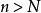
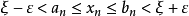
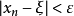
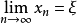
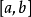


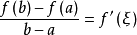
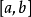


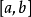
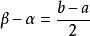
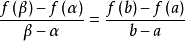
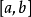
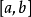
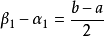
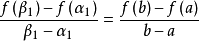
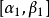
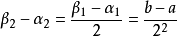
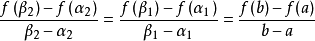
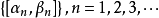

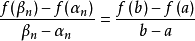
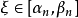
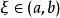
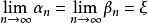
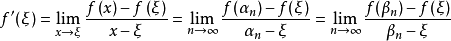
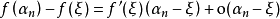
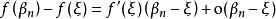
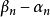
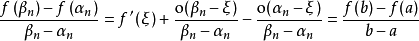
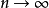
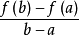
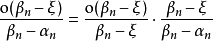
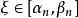

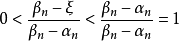
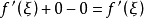
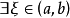
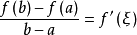
閉區間套定理:如果{[an,bn]}形成一個閉區間套,則在實數系中存在唯一的實數ξ屬於所有的閉區間[an,bn],n=1,2,3,…;即an≤ξ≤bn , n=1,2,3,…。...
閉區間的函式為小於等於的關係,即-∞≤a≤+∞,在數軸上為實心點。閉區間的余集(就是補集)是兩個開區間的並集。實數理論中有著名的閉區間套定理。...
有限覆蓋定理:設H是閉區間[a,b]的一個(無限)開覆蓋,則必可以從H中選擇有限個開區間來覆蓋[a,b]。有限覆蓋定理是一個有用而且重要的定理.它是數學分析處理...
而閉區間上連續函式的有界性定理的證明,在很多數學教材中,有多種方法可以證明此定理。比如可以利用閉區間套定理、確界定理、單調有界定理和柯西收斂準等。我們知道...
閉區間套定理 證明:不妨設 ,f(b)>0.令E={x|f(x)≤0,x∈[a,b]}.由f(a)<0知E≠Φ,且b為E的一個上界,於是根據確界存在原理,存在...
實數連續性定理包括:確界存在性定理,單調有界收斂定理,閉區間套定理,有限覆蓋定理,聚點定理,波爾查諾——魏爾斯特拉斯定理、柯西準則。 這七個定理可由確界存在...
但這裡有一個很微妙的問題,即與完備性公理等價的7個實數系的基本定理(確界存在定理、單調有界定理、有限覆蓋定理、聚點定理、緻密性定理、閉區間套定理和柯西收斂...
證明:零點定理可以利用閉區間套定理:如果{[an,bn]}是一個閉區間套,那么存在唯一實數ξ屬於所有的閉區間。詳細證法參考相應詞條。...
實數系的基本定理也稱實數系的完備性定理、實數系的連續性定理,這些定理分別是確界存在定理、單調有界定理、有限覆蓋定理、聚點定理、緻密性定理、閉區間套定理和...
由閉區間套定理,存在唯一實數 ,並且∴故數列 收斂,即級數 收斂。[1] 適用範圍注意,萊布尼茨定理所給出的條件(1)是充分非必要條件,即對非單調遞減的數列{un},...
可見序列(1)是一個退縮閉區間套,據退縮閉區間套定理,存在唯一實數 ,使下面證明 便是中介點 [2] 。設 ,如果 不是S的最大數,則必存在實數r∈S,使...
的閉區間 ,使 ;如此下去,得到一列閉區間,滿足:(1) ;(2) 的長度不超過 ,且 。因為 ,由數學分析中的閉區間套定理可知,存在唯一一點 。顯然有 ,由假設 應...
完備性公理可以換成閉區間套定理的形式。類似地,單調收斂定理,聚點原理等也可用作連續性公理。公理組II也有其他提法。用公理定義了實數系R後,可以繼續定義 R 的...
2.3.5 閉區間上的連續函式的性質?習題2.3第三章 實數及連續性3.1 實數的基本定理3.1.1 閉區間套定理3.1.2 有限覆蓋定理3.1.3 緻密性定理習題3.1...
6、《從有理閉區間套定理談起的問題》,獨著,待發。7、《一類耦合方程弱解存在性》,合著第一,待發。8、《談談數學分析與泛函分析的某些遞進關係》,獨著,第一...
