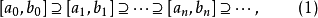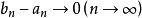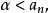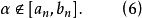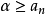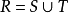戴德金原理

戴德金原理(Dedekind principle)亦稱戴德金分割，是保證直線連續性的基礎，其內容為：如果把直線的所有點分成兩類，使得：1.每個點恰屬於一個類，每個類都不空。2.第一類的每個點都在第二類的每個點的前面，或者在第一類里存在著這樣的點，使第一類中所有其餘的點都在它的前面；或者在第二類里存在著這樣的點，它在第二類的所有其餘的點的前面。這個點決定直線的戴德金割切，此點稱為戴德金點(或界點)，戴德金原理是戴德金((J.W.)R.Dedekind)於1872年提出來的，在構造歐氏幾何的公理系統時，可以選取它作為連續公理，在希爾伯特公理組Ⅰ，Ⅱ，Ⅲ的基礎上，阿基米德公理和康托爾公理合在一起與戴德金原理等價。

基本介紹

• 中文名：戴德金原理
• 外文名：Dedekind principle    
• 所屬學科：數學
• 所屬問題：高等幾何(幾何基礎)
• 別稱：戴德金分割
• 提出者：戴德金((J.W.)R.Dedekind)

基本介紹

定義1 若將實數集R分成兩個子集S和T，它們滿足：

(1)；

(2)；

(3)，總有x<y(稱S為左集，T為右集)

則稱為實數集R的一個“戴德金分劃”，記作(S，T)。

“戴德金分劃”的第一條要求是左集S與右集T都不是空集，也就是說它們中都有實數，簡稱為不空。第二條要求是S和T包含了所有的實數，換句話說，對於任何一個實數或者屬於左集S或者屬於右集T，二者必居其一，簡稱為不漏。第三條要求是左集S中的實數都比右集T中的實數小，簡稱為不亂。由第三條可以推知左集中的實數不會在右集中出現，右集中的數也不會在左集中出現。若x屬於左集，凡小於x的實數也都屬於左集，若y屬於右集，凡大於y的實數也都屬於右集。

例如令

讀者可以驗證(S，T)是一個戴德金分劃，再如令

S={x∈R | 存在自然數n，使}，

T={x∈R | x≥1}。

這也確定了一個戴德金分劃(S，T)。

第一個戴德金分劃中，左集S有最大數，而右集T沒有最小數；第二個戴德金分劃正相反，左集S沒有最大數，而右集T有最小數1。和1都叫做相應的戴德金分劃的中介點。一般說來，實數上的戴德金分劃必有中介點，下面的定理便說明這一點，而在有理數集上若類似地作一個戴德金分劃就不一定有中介點了。例如若令S={x∈Q | x≤0，或x²≤2)，T={x∈Q | x>0，且x²>2)則(S，T)構成對有理數集Q的戴德金分劃，但左集S無最大數；右集T無最小數，也就是(S，T)沒有中介點。

戴德金原理 實數集R的任一戴德金分劃(S，T)，都唯一地確定一個實數(稱為中介數或中介點)，它或者是S的最大數(此時T中無最小數)、或者是T的最小數(此時S中無最大數)。

戴德金原理的證明

在S中任取一數，T中任取一數b₀，由戴德金分劃的“不亂”性質，，閉區間的左端點屬於S；右端點屬於T，這樣的閉區間稱為入選區間，把二等分，設中點為c，則中必有一個且只有一個是入選區間，把它記作，再把二等分，而得到第三個入選區間，……這樣進分下去，便能得到一個入選區間組成的序列

因為這是逐一二等分得到的序列，所以

可見序列(1)是一個退縮閉區間套，據退縮閉區間套定理，存在唯一實數，使

下面證明便是中介點。

設，如果不是S的最大數，則必存在實數r∈S，使

又由於對每個n，b_n∈T，而r∈S，所以

由於，故對充分大的n，必有

對於端點滿足(5)式的閉區間，必有

即

否則，如果，與(3)，(4)兩式聯立起來，將有

將得到，與(5)式矛盾。但(6)式是與(2)式矛盾的。這個矛盾說明假設不是S的最大數是不對的，必為S之最大數。

S中有最大數，T中必無最小數，否則，若T中有最小數，則。由實數之稠密性，存在實數，使，但既不是S中的元素(因>S中的最大數)，又非T中的元素(因<S中的最小數)這與戴德金分劃的“不漏”性質()矛盾。

再設∈T，同理可證必為T中之最小數，且S中無最大數。

以上證明了每個戴德金劃分必有中介點，至於中介點的唯一性則是顯然的，若不然，有兩個中介點，那么當屬於S時，由於T中無最小數，所以不屬於T，由此可知屬於S，但S中的最大數當然只能有一個，所以。當屬於T時可同理得。