基本介紹
- 中文名:無窮小量
- 外文名:Infinitesimals
- 提出者:阿基米德
- 提出時間:公元前300年
- 套用學科:數學
- 適用領域範圍:數學分析
定義
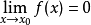



性質
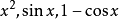
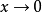

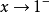
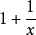


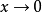
無窮大
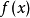


階的比較
前提條件




高低階無窮小量





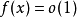

同階無窮小量


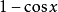



等價無窮小量




當x→0時
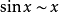

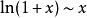
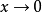

無窮小一般指本詞條
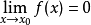



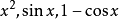
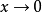

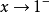
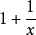


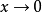
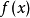











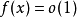



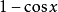







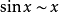

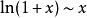
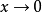
無窮小量是數學分析中的一個概念,在經典的微積分或數學分析中,無窮小量通常以函式、序列等形式出現。無窮小量即以數0為極限的變數,無限接近於0。確切地說,當...
等價無窮小是無窮小的一種。在同一點上,這兩個無窮小之比的極限為1,稱這兩個無窮小是等價的。等價無窮小也是同階無窮小。從另一方面來說,等價無窮小也可以看...
若lim(β/α)=0,則稱“β是比α較高階的無窮小”。意思是在某一過程(x→x0或x→∞這類過程)中,β→0比α→0快一些。...
《無窮小計算》是2012年高等教育出版社出版的圖書,由讓·亞歷山大·歐仁·迪厄多內編寫。本書可供大學數學專業師生選教,選學。也可供廣大數學工作者和相關專業人員...
若{an}是無窮小列,改變{an}中的某有限項之後,它仍是無窮小列。...... 若{ an}、{ bn}都是無窮小列,{ an+bn},{ an-bn}也是無窮小列。...
無窮小量,是極限為零的量,即若x→0時,limf(X)=0,則稱f(X)是當x→0時的無窮小量,簡稱無窮小。同階無窮小量,其主要對於兩個無窮小量的比較而言,意思是...
低階無窮小(Low order infinitesimal)是以數零為極限的變數,屬於高等數學學科。無窮小就是以數零為極限的變數。確切地說,當自變數x無限接近x0(或x的絕對值無限...
等價無窮小量指的是在兩個無窮小量在極限運算過程中等價代換。它對於極限的求解起到簡便運算作用。...
無窮小運算元(infinitesimal operator)亦稱無窮小生成元,是隨機過程理論的重要概念,它可對任意巴拿赫空間上的任一運算元半群來定義,是由運算元半群決定的閉線性運算元。...
若自變數x無限接近x0(或|x|無限增大)時,函式值|f(x)|無限增大,則稱f(x)為x→x0(或x→∞)時的無窮大量。例如f(x)=1/(x-1)^2是當x→1時的無窮...
在集合論中對無窮有不同的定義。德國數學家康托爾提出,對應於不同無窮集合的元素的個數(基數),有不同的“無窮”。兩個無窮大量之和不一定是無窮大,有界量與...
《法蘭西數學精品譯叢:無窮小計算》包含函式與映射的逼近及漸近展開式、複查解析函式的基礎、一階與二階線性微分方程的近似解法與穩定性以及貝寡爾函式等。書中有不...
《數學物理趣談—從無窮小開始》是2015年科學出版社出版的圖書,作者是張天蓉。...... 《數學物理趣談—從無窮小開始》是2015年科學出版社出版的圖書,作者是張天蓉。...
歐拉的《無窮小分析引論》是數學七大名著之一, 和高斯的《算術研究》齊名。...... 歐拉的《無窮小分析引論》是數學七大名著之一, 和高斯的《算術研究》齊名。...
某一負數值表示無限小的一種方式,沒有具體數字,但是負無窮表示比任何一個數字都小的數值。 符號為-∞。 數軸上可表示為向左無限遠的點。 表示區間時負無窮的...
兩個無窮大相除的極限為1,則稱其為等價無窮大。...... 等價無窮大的倒數為等價無窮小。若一極限存在,在此極限過程中的等價無窮大可相互替換。...
古希臘哲學家亞里士多德(Aristotle,公元前384-322)認為,無窮大可能是存在的,因為一個有限量是無限可分的,但是無限是不能達到的。12世紀,印度出現了一位偉大的數學...
1 朗道符號 ▪ 無窮大漸近 ▪ 無窮小漸近 2 常用的函式階 大O符號朗道符號 編輯 大O符號是由德國數論學家保羅·巴赫曼(Paul Bachmann)在其1892年的著作...
第二次數學危機是由無窮小量的矛盾引起的,它反映了數學內部的有限與無窮的矛盾。數學中也一直貫穿著計算方法、分析方法在套用與概念上清楚及邏輯上嚴格的矛盾。在...
隨機變數,(小)區間內的一個未知特定值 15 Ο ο /əuˈmaikrən/ 或/ˈɑmɪˌkrɑn/ omicron 歐(阿~)米可榮 高階無窮小函式 16 ...
洛必達法則是在一定條件下通過分子分母分別求導再求極限來確定未定式值的方法。眾所周知,兩個無窮小之比或兩個無窮大之比的極限可能存在,也可能不存在。因此,求...
魏爾斯特拉斯用排除無窮小量的辦法來解決貝克萊悖論,而在上世紀60年代,魯濱遜又把無窮小量請了回來,引進了超實數的概念,從而建立了非標準分析,同樣也能精確地...
沃利斯是英國數學家、物理學家,沃利斯是最先把圓錐曲線當作二次曲線加以討論的人之一。主要著作有:《圓錐曲線論》、《無窮小算術》、《論擺線》、《代數學》、...
數學史上把貝克萊的問題稱之為“貝克萊悖論”。籠統地說,貝克萊悖論可以表述為“無窮小量究竟是否為0”的問題:就無窮小量在當時實際套用而言,它必須既是0,又不是...
