同階無窮小

無窮小量，是極限為零的量，即若x→0時，limf(X)=0，則稱f(X)是當x→0時的無窮小量，簡稱無窮小。同階無窮小量，其主要對於兩個無窮小量的比較而言，意思是兩種趨近於0的速度相仿。

基本介紹

• 中文名：同階無窮小
• 外文名：Infinitesimal of the same order
• 意義：兩個無窮小的階數比較
• 函式值：與零無限接近
• 一級學科：數學
• 二級學科：高等數學

無窮小量

如果在x→0時，f(X)=0，則稱f(X)=0是當x→0時的無窮小量，簡稱無窮小。

無窮小量就是極限為零的量。確切地說，當自變數x無限接近x0(或x的絕對值無限增大)時，函式值f(x)與零無限接近，即limf(x)=0，則稱f(x)為當x→x0(或x→∞)時的無窮小量。例如，f(x)=(x－1)^2是當x→1時的無窮小量，f(x)= 1/n是當n→∞時的無窮小量，f(x)=sinx是當x→0時的無窮小量（注意：特別小的數和無窮小量不同）。

同階無窮小

如果lim F(x)=0,lim G(x)=0,且lim F(x)/G(x)=c，c為常數並且c≠0，則稱F(x)和 G(x)是同階無窮小。例如：

計算極限：lim（1-cosx）/x^2在x→0時，得到值為1/2，則說在x→0時，（1-cosx）與x^2是同階無窮小。

例如，因為

所以，在 x→3 的過程中，x²-9 與 x-3 是同階無窮小。意思是在x→3 的過程中，(x²-9)→0 與 (x-3)→0的快慢一樣。

無窮小的比較

觀察無窮小比值的極限：

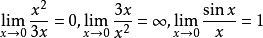
兩個無窮小比值極限的各種不同情況，反映了不同的無窮小趨於零的“快慢”程度。在x→0 的過程中，x^2→0 比 3x→0 “快些”，反過來 3x→0 比 x^2→0 “慢些”，而 sin x→0 與 x→0 “快慢相仿”。

為了套用上的需要，我們就無窮小之比的極限存在或為無窮大時，給出下面的比較定義。

定義，設 α 及 β 都是同一個自變數的變化過程中的無窮小。

如果，就說β是比α高階的無窮小，記為；

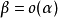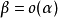
如果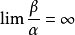，就說β是比α 低階的無窮小；

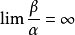
如果，就說β與α 是同階無窮小；

如果，就說β是關於 α 的k階無窮小；

如果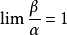，就說β與α 是等價無窮小，記為 β~α。