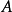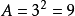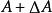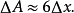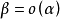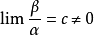基本概念
對於兩個
無窮小量
和
,如果
,就把
叫做比
高階的無窮小量,並把
叫做比
低階的無窮小量;簡稱
是
的
高階無窮小,
是
的低階無窮小,記成
。
如果
,其中
為異於零的
常數,這時把
叫做
的
階無窮小。
例如,因為
,所以
時
是比
較高階的無窮小,意思是說在
的過程中
比
趨向0的速度快。
概念分析
在同一個變化過程中的兩個無窮小,雖然同時都趨向於零,但是它們趨向於零的快慢程度有時卻不一樣,甚至差別很大。實際問題中,有時需要討論這種趨向零的快慢問題,舉例於下。
 圖1
圖1有一塊正方形的金屬片,它的邊長原來是3,受熱後增加了
,問這塊金屬片的面積增加了多少?
如圖1所示,設加熱前正方形金屬片的面積為
,即
,加熱後正方形金屬片的面積為
,即
這個等式的右邊有兩項,我們在圖1中看到,畫有斜線的兩塊窄矩形的面積之和就是
,而畫有交叉線的一小塊正方形的面積就是
。
容易看出,當
時
,就是說,
和
都是當
時的無窮小。現在我們把它們趨近於零的快慢情況列表比較於下:
| 0.5 | 0.1 | 0.01 | 0.001 | ...... | → 0 |
| 3 | 0.6 | 0.06 | 0.006 | ...... | → 0 |
| 0.25 | 0.01 | 0.0001 | 0.000001 | ...... | → 0 |
從表中看出,當
時,
趨近零比
趨近零快得多,從它們的比值來看,就有
即
與
之比也是當
時的無窮小。這時,我們就說
是比
高階的無窮小。
一般地,我們對兩個無窮小的比較作如下規定:
設
和
都是無窮小,如果
,我們就說
是比
高階的無窮小。
在實際問題的計算中,如果遇到幾個不同階的無窮小量之和,常常把高階無窮小忽略不計。例如,在計算上述正方形金屬片加熱後的面積時,如果
不大,就往往略去
項,而得到
這樣,既抓住了主要矛盾,又簡化了運算手續,而且在許多情況下滿足了實際問題的要求。
無窮小量的比較
設
是同一變化過程中的無窮小,
這一過程中的極限,那么:
常用的等價無窮小
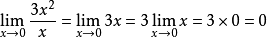






 圖1
圖1