基本介紹
- 中文名:交運算
- 所屬學科:數學
- 相關概念:格,集合的交,偏序集等
關於格的交運算

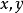





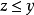
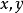
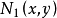



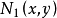
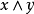

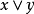


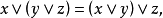
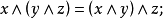

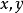
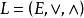



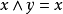


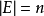
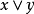
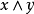
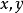


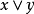
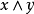
集合的交運算
定義
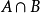
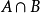

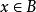
舉例說明
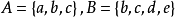



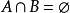
例如:
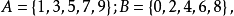
圖形表示
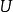
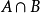
 圖1 集合的交運算
圖1 集合的交運算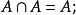
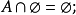

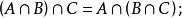
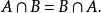



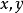





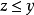
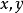
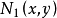



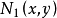
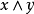

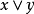


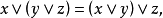
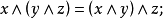

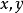
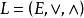



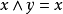


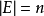
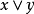
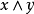
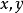


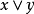
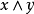
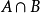
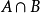

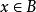
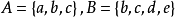



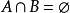
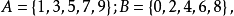
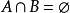
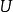
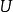
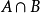
 圖1 集合的交運算
圖1 集合的交運算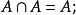
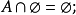

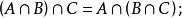
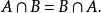

交運算有兩種含義,它可以指集合的交運算,即兩個集合的交集,與之對應的是集合的並運算,即兩個集合的並集;也可以指格的交運算,與之相對應的是格的結運算。...
運算律是通過對一些等式的觀察、比較和分析而抽象、概括出來的運算規律。既是重要的數學規律,也是數學運算固有的性質。包括加法交換律和結合律、乘法交換律和結合律...
基本運算是指執行運算最基礎的算法。在關係代數運算中,有5種基本運算,它們是並(U)、差(—)、投影、選擇、笛卡爾積(X),其它運算即交、連線和除,均可通過5種...
交集運算 編輯 (1)若兩個集合A和B的交集為空,則說他們沒有公共元素,寫作:A∩B = ∅。例如集合 {1,2} 和 {3,4} 不相交,寫作 {1,2} ∩ {3,4}...
Λ 是邏輯運算的一種符號。第十一個希臘字母,讀音為Lambda(小寫λ),英語發音為:['læmdə]。...
交集合是指對於集合A和集合B,由即屬於A又屬於B的所有元素所組成的集合。...... 叫做集合的交運算,交運算是集合代數中的最基本的運算之一,相當於算術中的乘法,...
概念:兩條直線軌道在同一平面上相交所形成的區域叫交叉。 交叉設備:是道岔中的...信號控制交叉口通行能力的計算方法主要有以下4種:①飽和流率法;②停止線法;③...
積集亦稱交集,集合論的基本概念之一,指兩個(或多個)集合經交運算所得到的集合。對於任意兩個集合 A 與 B,由既屬於 A 又屬於 B 的元素所組成的集合 C ,...
交點計算方法 編輯 兩條直線相交,有一個交點。三條直線兩兩相交最多有3個交點,四條直線兩兩相交最多有6個交點,五條直線兩兩相交最多有10個交點......
集合E的全體子集之集P(E)的任一非空子集, 如果它對有限並及差的運算是穩定的,則稱它為集合E的集(合)環, 從而集環對於有限交運算亦是穩定的,例如,R上兩...
例如集合 {1, 2} 和 {3, 4} 不相交,寫作 {1, 2} ∩{3, 4} = Ø。 更一般的,交集運算可以對多個集契約時進行。 例如,集合 A,B,C 和 D ...
集合布爾代數(Boolean algebra of sets)亦稱集合布爾格、集合格,是一種特殊的格,指以集合為元素的格,全集I的冪集P(I)對交、並運算是封閉的,對包含於關係“...
π類(π-class)是對交運算封閉的集類。引入π類、λ類的概念,對掌握σ環和σ代數特別是某些集類生成的σ環和σ代數頗有幫助。...
如上所述集合套的並、交、補。集合套的並、交運算就是用經典集合的並、交來定義的,因此模糊集保持關於並、交運算的性質就是自然的事了。同時,也因為集合套的...
使用全站儀進行工程測量時,測量至兩個坐標已知點的距離,即可計算出全站儀的坐標。此即為測邊交會。中文名 測邊交會 目錄 1 定義 2 點位排列順序 3 計算公式...
後方交會是指僅在待定點上設站,向兩個個已知控制點觀測一個水平夾角A,從而計算待定點的坐標,稱為後方交會。交會測量是加密控制點常用的方法,它可以在數個已知...
確定有限狀態自動機的交,並,差,補,連線,替換,同態,逆同態等運算是封閉的,也就是說確定有限狀態自動機通過這些運算產生的新的自動機也是確定有限狀態自動機。 [2...
半格(semilattice)格的推廣.它是只關聯到格的結運算和交運算二者之一的一類代數結構.對於格z= cx; v , n)而言,只關聯到結運算的半格,稱為結-半格,記為...
簡單性是指包圍盒間進行相交測試時需要的計算量,這不但要求幾何形狀簡單容易計算,而且要求相交測試算法簡單快速;緊密性要求包圍盒儘可能的貼近被包圍的對象,這一屬性...
1 示例數據 2 計算方法 不完全雙列雜交示例數據 編輯 [2] 數據見作物數量遺傳學基礎——六、配合力:不完全雙列雜交這篇文章的數據,用GenStat軟體進行處理。不...
這幾年,分散式凸交計算(Distributed convex intersec-tion computation)越來越受到研究人員的重視,並在包括圖像重構中原像的恢復、凸投射的最佳逼近和目標定位等實際...
特別地,當L是格時,可以定義兩個L模糊子集A與B的並、交運算如下:如果L是完備格,則並、交運算可推廣到任意多個L模糊子集的情形...
1 名詞解讀 2 交割申報 3 交收規定 4 延期補償 5 機制優勢 6 計算方式 7 滿足需求 8 方式比較 現貨連續交易名詞解讀 編輯 連續:1...
