∩

∩是是高中數學學習的集合當中常用的符號。

由所有屬於集合A且屬於集合B的元素組成的集合，叫做A，B的交集。

基本介紹

• 中文名：∩（交）
• 簡介：交集符號
• 例子：A和B的交集寫作A∩B，讀作A交B
• 詞性：名詞
• 數學定義：A∩B={x|x∈A且x∈B}
• 學科：數學
• Latex表示：\cap

基本定義

A 和 B 的交集寫作 "A ∩B"。表示：A 交 B形式上：

Ax+b=y-a

x 屬於 B。

例如：集合 {1, 2, 3} 和 {2, 3, 4} 的交集為 {2, 3}。 數字 9 不屬於素數集合 {2, 3, 5, 7, 11, …} 和奇數集合 {1, 3, 5, 7, 9, 11, …} 的交集。

若兩個集合 A 和 B 的交集為空，就是說他們沒有公共元素，則他們不相交，寫作：A ∩B = Ø。例如集合 {1, 2} 和 {3, 4} 不相交，寫作 {1, 2} ∩{3, 4} = Ø。

更一般的，交集運算可以對多個集契約時進行。 例如，集合 A，B，C 和 D 的交集為 A ∩B ∩C ∩D = A ∩(B ∩(C ∩D))。 交集運算滿足結合律，即

A ∩(B ∩C) = (A ∩B) ∩C。

任意交集

最抽象的概念是任意非空集合的集合的交集。 若 M 是一個非空集合，其元素本身也是集合，則 x 屬於 M 的交集，若且唯若對任意 M 的元素 A，x 屬於 A。 符號表示為：

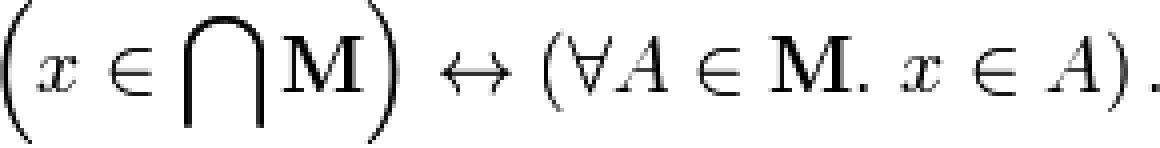
這一概念與前述的思想相同，例如，A ∩B ∩C 是集合 {A,B,C} 的交集。 （M 何時為空的情況有時候是能夠搞清楚的，請見空交集）。

這一概念的符號有時候也會變化。 集合論理論家們有時用 "∩M"，有時用 "∩A∈M A"。 後一種寫法可以一般化為 "∩i∈I Ai"，表示集合 {Ai : i ∈ I} 的交集。 這裡 I 非空，Ai 是一個 i 屬於 I 的集合。

當索引集 I 為自然數集合時，這種符號表示與無限序列相類似：

為了排版方便，上述符號也可以寫成 "A1 ∩ A2 ∩ A3 ∩ ..."，即使用嚴格的寫法 A1 ∩ (A2 ∩ (A3 ∩ ... 也沒有區別。（這個例子是可數個集合的交集，非常常用；作為一個示例，請參看σ-代數。）

最後，注意當符號 "∩" 寫在其他符號之前，而不是之間的時候，需要寫得大一號。（在HTML中，可以使用字型 &bigcap;，或者嘗試 <big>&cap;</big>。）

輸入方法

用搜狗打字法拼出“jiaoji”或“jiao”選5就行了。

用QQ拼音打字法拼出“jiaoji”選5就可以了。

QQ五筆輸入 zzbd 然後再按7下翻頁再選5就是。

在微軟輸入法中拼出jiaoji再按6就可以了