原理簡介 第一個常用的公理系統是E.F.F.
策梅洛 和A.A.
弗倫克爾 等提出的ZF系統。這個系統中只有一個非邏輯
二元關係 符號∈,非邏輯公理有:
外延公理 、
空集公理 、無序對公理、並集公理、冪集公理、無窮公理、
分離公理模式 、替換公理模式、正則公理。如果加上選擇公理就構成ZFC系統。利用公理可以定義出
空集 、序對、關係、函式等集合,還可以給出序關係、良序關係、序數、基數,也可以給出自然數、整數、實數等概念。
通過
元語言 ,也可公理系統中各公理之間的相容性和獨立性,例如Cohen於1960年創立公理集合論中的
力迫法 ,並用來證明
ZFC 與
連續統假設 CH獨立。公理集合論發展很快,馬丁公理、蘇斯林假設等新公理新方法已被廣泛使用,組合集合論、
描述集合論 、大基數、力迫法的研究也持續發展。
詳細內容 一定要注意的一點:
ZF公理系統 中,集合的元素都是集合,自然數可用
皮亞諾公理 系統表示,如3={0,1,2}={{},{{}},{{},{{}}}}。
ZF公理系統:
(ZF1)外延公理:一個集合完全由它的元素所決定。如果兩個集合含有同樣的元素,則它們是相等的。
(ZF2)
空集 合存在公理:即存在一集合s,它沒有元素。
(ZF3)無序對公理:也就是說,任給兩個集合x、y,存在第三個集合z,而w∈z若且唯若w=x或者w=y。
註:z = {x, y}, 就是說,如 w∈z, 則 w=x 或 w=y。又名配對公理,取義可由二個集合生成第三個集
合,集合無次序(或說生成的第三個集合無次序),所以叫無序(配)對公理,就一個,如果有次序
就變二個了。
(ZF4)
並集公理 :也就是說,任給一集合x,我們可以把x的元素的元素匯集到一起,組成一個新集合。
準確的定義:“對任意集合x,存在集合y,使w∈y若且唯若存在z使z∈x且w∈z”。
(ZF5)
冪集公理 :也就是說,任意的集合x,P(x)也是一集合。
準確的定義:“對任意集合x,存在集合y,使z∈y若且唯若對z的所有元素w,w∈x”。
(ZF6)無窮公理:也就是說,存在一集合x,它有無窮多元素。
準確的定義:“存在一個集合,使得空集是其元素,且對其任意元素x,x∪{x}也是其元素。”
根據皮亞諾公理系統對自然數的描述,此即:存在一個包含所有自然數的集合。
(ZF7)
替換公理模式 :也就是說,對於任意的函式F(x),對於任意的集合t,當x屬於t時,F(x)都有定義(ZF中唯一的對象是集合,所以F(x)必然是集合)成立的前提下,就一定存在一集合s,使得對於所有的x屬於t,在集合s中都有一元素y,使y=F(x)。也就是說,由F(x)所定義的函式的
定義域 在t中的時候,那么它的值域可限定在s中。
(ZF8)
正則公理 :也叫基礎公理。所有集都是
良基集 。說明一個
集合 的元素都具有最小性質,例如,不允許出現x屬於x的情況。
準確的定義:“對任意
非空集合 x,x至少有一元素y使x∩y為空集。”
註:(ZF3)可以由其他公理導出,所以有些場合不出現這條公理,與之類似的是“
子集 公理”。
(AC)
選擇公理 :對任意集c存在以c為
定義域 的選擇函式g,使得對c的每個非空元集x,g(x)∈x。
ZF集合公理系統加上AC就成為ZFC公理系統。
註:ZF為Zermelo及Fraenkel
替換公理 如果一集合
x 的元素的元素也都還是
x 的元素,則稱
x 為傳遞集。一個集合
x 是自然數:如果
x 是傳遞集,
x 的全體元素在∈下
良序 ,而且
x 的每一
非空子集 對序∈而言有最大元。這樣可以把自然數變成了在ZF內可以定義的一種性質,如把0定義作空集═,1定義作0∪{0},2定義作1∪{1}……等等,則0,1,2,…,都是自然數,而且只有這些是自然數。
自然數 “
x 是
序數 ”是指如果集合
x 是傳遞集,而且
x 在∈下
良序 。令
O n表示全體序數所成的集合,
α ,β∈
O n,
α <
α ∈
β 。這樣,就用∈定義了序數間的< 關係,每一序數都是由比它自身小的序數所組成的
集合 。
每一自然數都是序數,全體自然數{0,1,2,…}也是序數。對任一集合
x ,令
s (
x )=
x ∪{
x }。則當
x 是序數時,
s (
x )亦為序數。一序數
α 稱作
後繼序數 :如果有一序數
β ,使
α =
s (
β )。不是後繼序數的序數稱為極限序數,例如0,
ω 均為
極限序數 O n雖為一真類,但<O n,<>;具有性質:O n的任一非空子類都有最小元。因此,要想證明每一序數都具有性質φ ,即可套用超限歸納原理:對於任給的一序數β ,若每一比β 小的序數α 都具有性質φ 則β 亦具有性質φ ,那么對所有的序數都具有性質φ 。
在定義序數運算(加、乘、冪)時,需要用超限遞歸定理:若
G 是一運算,則有一運算
F ,使得對每一序數
α ,都有
F (
α )=
G (
α )。而這一定理的證明要用到替換公理。有了替換公理還可以得到極限序數
ω +
ω 的存在性。如果先將正整數從小排到大,再把
非正整數 從大排到小而成一序列:1,2,3,…,0,-1,-2,…。從而全體整數就良序了,其序型即為
ω +
ω 。
事實上,任一良序集〈
ω ,<;〉,都有惟一的序數
α 使得〈
w ,<;〉序同構於〈
α ,∈〉。因此,就可以把
良序集 按
序同構 來分類,並將同屬於一類的稱為具有同一序型的良序集。而序數就可定義作為同構的良序集的代表。依此,可以定義序數的運算。例如,序數的加法可以定義如下:若
α ,
β 為序數,
γ 為
極限 序數
β +0=β ,β +s (α )=s (β +α ),β +γ (β +α ),即用關於α 的超限歸納原理來定義β +α 。同樣地可以定義序數的積β .α 和冪β α,以及相應的運算性質,如結合律等。 可以證明:替換公理是獨立於其他公理的。
正則公理 正則公理 與其他公理不同,它不是斷言某些集合的存在,而是限制一些集合的存在。提出它是為了研究ZF的模型。在ZF中可定義的數學對象都不以自身為元素;也未發現有集合
x ,
y ,具有
x ∈
y 並且
y ∈
x 的性質或者集合序列
x 1,
x 2,…,滿足:。1917年 D.米里馬諾夫首先提出良基集的概念。1922年弗倫克爾在
策梅洛 原來的公理系統補充了一條公理名曰限制公理,顧名思義,它是給出某種限制,以排除那些非良基集。1925年J.馮·諾伊曼,稱它為正則公理。1930年策梅洛也獨立地引入了這條公理,並稱它為基礎公理。從而完成了ZF。
馮·諾伊曼給出了一個分層其中
V 0=═(
α 為任一序數,F(
V α)表
V α的冪集。這樣,正則公理肯定了每一集合必在某一
V α中。若再引進
γ,稱為 x 的秩。從而,即可依秩來作超限歸納。
公理集合論 在AC成立的條件下,每一群都同構於一個在
π 中的群:每一
拓撲空間 都同構於一個在Π中的拓撲空間,等等。而在數學討論中常常是把同構的對象視作同一的;故正則公理並不給討論帶來局限。
基數 基數概念至為重要。兩個集
x 、
y 稱作是
等勢 若在
x 與
y 之間能建立一個一一對應。如果集合
x 與
y 等勢,則記作
x ~
y 。由於AC任一
集合 x 都可以
良序 化,故有
序數 α ,使得
α ~
x ,把這種
α 中最小的那個序數定義作為集合
x 的基數,並記作│
x │。這樣定義的基數│
x │仍然是一個集合;而每一集合
x 都有一個│
x │作為
x 的數量大小的一個刻畫;並且如果
x ~
y ,則│
x │=│
y │。
兩個集x、y稱作是等勢的 這樣定義的基數是序數的一部分:即是不能與小於自己的序數等勢的那些序數,也就是所謂初始序數。例如0,1,2,…,ω 等都是初始序數,因而都是基數。而ω +1,ω +2,…,ω +ω 等都不是初始序數,故都不是基數。所以緊接著基數0,1,2,…,ω 的基數是ω 1,它也記作堗1。
如果AC不成立,則可利用正則公理來定義任一集合
x 的基數,記作憫。憫為一集合:。 上述定義系D.S.斯科特於1955年給出的。
公理集合論 在60年代末期A.萊維還證明了在AC與正則公理都不成立的情況下,基數概念是不可定義的。
構造模型 由哥德爾不完備性定理可知:如果ZF是協調的,則在ZF中不能證明自身的協調性。所以,在公理集合論中只考慮相對協調性問題。如:解決這類問題的常用方法就是構造模型。在公理集合論中構造模型的方法不外三點:內
模型法 ,外模型法(即力迫方法),對稱模型法。
公理集合論 內模型法 是從已知的一個模型M 出發,來定義M 的一個子模型M s;使得M s滿足ZF的一些公理或者ZF以外的一些公理。
公理集合論 的一個著名成果就是1938年K.哥德爾所給出的
ConZF→Con(ZF+CH)的證明,證明中用的就是內模型法,但是當時尚未如此命名。
迄至1951年J.C.謝潑德森已經把內模型法研究得很完善,並已知道要用此法去證明是不可能的。
公理集合論 外模型法(即
力迫法 )是P.J.科恩1963年所創,科恩據此而證明了CH的相對於ZF的獨立性。
排列模型的想法始於弗倫克爾,當時他是用來證及一些弱
選擇公理 的相對協調性,適用於有原子(本元)的集合論。迭經A.莫斯托夫斯基、斯派克等人的改進而形成FMS方法,其與外模型法相結合即可構成對稱模型法。
公理集合論 分支 簡介 在公理集合論的研究中,大量的工作是關於集合論模型的,此外,還繼續此前
樸素集合論 對無窮組合問題的研究即組合集合論的研究。其中的一些問題是來源於柯尼希樹引理和 F. P.
拉姆齊 定理的推廣。另一分支則為
描述集合論 (亦稱解析集合論),主要是研究劃分層次以後的
實數 子集 的結構性質問題。因而,這一部分與分析、
實數理論 和
遞歸論 的關係較為密切。
即使限於上述兩個分支的研究,也有許多問題要用到ZF(或ZFC)以外的附加假設才能判定。這裡,常用的附加假設有:可構成公理;各種大基數公理,以及與AC不協調的決定性公理等。
哥德爾在1938年提出了可構成公理,並在60年代末和70年代得到重視和發展。至於大基數的研究由來已久,但其作為附加公理亦是在60年代以後。幾乎每一種大基數都是ω 的某種性質向不可數基數的推廣。可構成性、大基數和力迫法已成為公理化集合論的三大主流,同時它們又是三種研究工具。隨著無窮博弈的誕生和博弈論在數學各分支的滲透,以及博弈論與邏輯的關係日益密切,決定性公理也愈受到重視。
選擇公理 選擇公理 是
現代數學 中最常用的假設,過去許多人曾不自覺地使用。對這個問題引起注意,是因為
康托爾 在1883年提出任意集合是否都可良序化的問題。希爾伯特也曾把這個問題引入其23問題頭一問題的後半部分。1904年,策梅羅提出選擇公理,並通過選擇公理證明了
良序定理 。這個公理有極多的等價形式,其中有在
代數 中常用的造恩引理。這個套用極廣、看來正確的選擇公理,卻可以證明出一些看來荒唐的結果。如1914年的豪斯道夫的分球面定理和U23年的巴拿赫—塔爾斯基
悖論 。
可是選擇公理的用途太大,不能忽視,許多學科的基本定理少不了它:
泛函分析 中的哈恩—巴拿赫定理(關於
巴拿赫空間 上的
線性 泛函的可擴張性);拓撲學的吉洪諾夫定理(關於任意多緊空間的
直積 為緊);布爾代數的斯通表示定理,每個布爾代數皆同構於集代數;自由
群論 的尼爾森定理,自由群的子群也是自由的。
其他還有許多定理,如果沒有選擇公理也不行。
連續統假設 連續統假設 的歷史最久,它可以說是隨著集合論一起產生的。1883年
康托爾 就提出了這個假設,可數無窮集的基數的後面就是連續統的基。康托爾花了畢生精力去證明,但沒有成功。希爾伯特把它列入自己著名的23個問題的頭一個。希爾伯特本人也曾經用了許多精力證明它,並且在192~—1926年宣布過證明的大綱,但終究未能成功。這個問題終究懸而未決。
1930年哥德爾完成了他的兩大貢獻以後,曾說過“現在該輪到集合論了”。他從1935年起就開始研究連續統假設及廣義連續統假設。這一次他又出人意料地證明了ZF和GCH是協調一致的,不過當然要假設ZF本身也是協調的,雖然這一點一直沒有得到證明。
哥德爾套用可構造性公理證明ZFC和ZFC+GCH的相對無矛盾性,他用可構造集的類L作為ZFC的模型。1963年7月,美國年輕數學家科恩發明了影響極為重大的力迫法,並證明連續統假設的否定命題成立,這樣一來CH在ZF中既不能證明也不能否定。
可構成性公理 哥德爾證明選擇公理和連續統假設協調性的方法是定義一種類型的集合,叫做可構成集。假如把集合論中集合的概念完全用可構成集合的概念來理解,那么集合論中的一些概念就會有相應的改變。但是有一些概念不會改變,這種概念我們稱為絕對的,特別是可構成性這個概念是絕對的。所以“一切集合是可構成的”,這稱為可構成性公理。
可構成性 的概念非常重要,表現在:
3、如果可測基數存在,則不可構成集合存在,這是斯科特1961年證明的。隨後,羅巴通在他1964年的博土論文中證明可測基數的存在,蘊涵整數不可構成集合的存在性,後來他又證明可測基數的存在蘊涵只有可數無窮多個整數的可構成集合。
馬丁公理 馬丁公理 是1970年由馬丁等人提出來的,它與ZFC的其他
公理 完全不同,不像一個“真”的公理,但是由它可以推出數學上重要的結果。馬丁公理是
連續統假設 的推論,因此可以看成是弱連續統假設。
馬丁公理在數學上有一系列的重要套用。特別重要的是,
舍拉 在1974年證明
懷特海 猜想 在
ZFC 下是不可判定的。同樣,許多
拓撲學 問題也有類似情況。
大基數公理 連續統假設及廣義連續統假設反映了最理想的大基數產生的方法,也就是一個接一個由
冪集 的基數產生出來。但是,這種理想的情況無法證明,而與它不同或矛盾的情形也不可能得到否定。因此,這種種特殊大基數的存在性能得到更加特殊的結果,而且對數學本身產生了不可忽視的影響。
雖然這些大基數極為玄乎,可是由它們可以推出許多重要的數學結果。因此我們不得不重視它,而它們的存在性作為公理就是大基數公理。可以料到這些大基數公理同原來的一些公理是矛盾的。比如,可構造公理就蘊涵可測基數不存在。
大基數公理對數學問題的重要性可以由下面問題的解決看出:拓撲學中一個著名的幾十年末解決的正規莫爾空間猜想歸結為可測基數的存在問題,而象過去局限於ZFC系統的證明是沒有希望的。
決定性公理 決定性公理是與描述集合論密切相關的公理,它涉及到
自然數列 的集合是否能夠通過某種方法決定。決定性公里的基本問題是:什麼集合是可決定的?經過許多人的努力,馬丁在1975年證明,數學中最常用的保萊爾集合是可決定的。下一個猜想是證明所有解析集合(即
二維 保萊爾集合的
射影 集合)是可決定的,但這個猜想與哥德爾的可構成性公理相矛盾。上面講過,可構成性公理是與ZFC是相容的,因此這個猜想無法在集合論中證明。這樣一來,它本身可以成為一個
新 公理 。
比這個公理更加激進的公理是:R的所有子集合都是決定的。這個公理太過激烈了,以致很難為“真”,因為它首先同選擇公理有矛盾。不過,由這個決定性公理卻能推出一系列有趣的數學事實;其中最突出的是,由它可推出所有
實數集 合 都是
勒貝格 可測的。這樣一來,許多數學成為沒有意思的了。因此,數學家還是不太想要這個太強的公理。可是,它帶來的一系列問題仍有待解決。
 公理集合論
公理集合論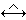 兩個集x、y稱作是等勢的
兩個集x、y稱作是等勢的 公理集合論
公理集合論 公理集合論
公理集合論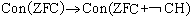 公理集合論
公理集合論 公理集合論
公理集合論
 公理集合論
公理集合論 兩個集x、y稱作是等勢的
兩個集x、y稱作是等勢的 公理集合論
公理集合論 公理集合論
公理集合論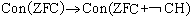 公理集合論
公理集合論 公理集合論
公理集合論