基本介紹
定義,基本蘊含,拓展,
定義
從這個公理可得出兩個結果，其一為“不存在以自身為元素的集合”，其二為“沒有無限序列an使得對於所有i，ai+1是ai的元素”。通過選擇公理可以證明後者的逆命題也成立：如果這樣的無限序列不存在，則正則公理為真。所以在假定選擇公理的情況下，兩個陳述是等價的。
正則公理被認為是Zermelo-Fraenkel 集合論中套用最少的公理，因為數學分支中的所有關鍵性結果都可用集合論中的其他公理證明得到。另外，不包含正則公理的康托的集合論，實際上假定了以自身為一個元素的集合（真類）的存在。
基本蘊含
不存在以自身為元素的集合
反證，假設有一個非空集合A，使得A是自身的一個元素，即
。這時，根據配對公理，可以構造出
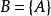，B也是一個集合。由於只有
，根據正則公理，我們得到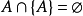
。但是根據我們的假定有 及 ，所以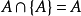
。這與正則公理相矛盾！所以不存在這樣的集合A。
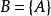
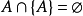
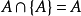
不存在無限遞降的集合序列
設f為一定義在自然數集上的函式，且對每個n，f(n+1) 都是f(n) 的一個元素。定義f的值域S= {f(n):n是自然數}，按照函式的形式定義S是一個集合。對S套用正則公理，可知S中有一個元素f(k)，其與S不相交。但按照f和S的定義，f(k) 和S有一個公共元素（就是f(k+1)）。這是個矛盾，所以不存在這樣的f。
注意這個論證只有在集合（而非不可定義的類）的情況下才對f適用。繼承有限集合Vω是滿足正則公理的，所以如果你構造Vω的一個非平凡的超冪，那么它也會滿足正則公理，但是，它會包含無限遞減的元素序列。例如，假定n是非標準自然數，則有
，如此類推，對於任何標準的自然數k有
。所以這是個無限遞降的元素序列。但是這個序列在這個模型中是不可定義的，因此它並不是集合，也就沒有違反正則公理。
假定選擇公理，則"無限遞減的集合序列不存在"蘊涵正則公理
設非空集合S是正則公理的一個反例；就是說S的所有元素都與S有非空交集。設g是S的選擇函式，就是說對於S的每個非空子集s，g會把s映射到s自身的一個元素。然後，在非負整數上遞歸的定義函式f為如下：
（1）
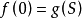
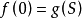
（2）
那么對於每個n，f(n) 是S的一個元素，因此它與S的交集是非空的。從而f(n+1) 是良好定義的，並且是f(n) 的一個元素。所以f是一個無限遞降的鏈。這是一個矛盾，所有這樣S不存在。
確使有序對 (a,b) 可定義為 {a,{a,b}}
這個定義消除了有序對的 Kuratowski 規範定義 (a,b) = {{a},{a,b}} 中的一對花括弧。
