並集公理可以得出包含公理:對任意兩集 X 與 Y,存在同時以 X,Y 為子集的集合。
基本介紹
- 中文名:包含公理
- 外文名:axiom of inclusion
- 適用範圍:數理科學
簡介
引入



定義

策梅洛-弗蘭克爾集合論
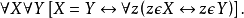
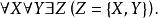
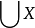


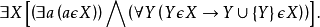
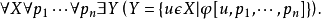

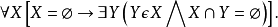
並集公理可以得出包含公理:對任意兩集 X 與 Y,存在同時以 X,Y 為子集的集合。




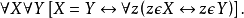
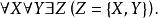
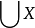


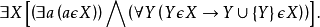
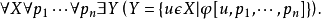

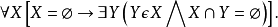
並集公理可以得出包含公理:對任意兩集 X 與 Y,存在同時以 X,Y 為子集的集合。...... 並集公理可以得出包含公理:對任意兩集 X 與 Y,存在同時以 X,Y 為子...
集合存在性公理(existence axiom of set)是GB系統的集合論公理,指GB系統中的第3組(即C組)公理,共有4條,包括無窮公理,並集公理,冪集公理,和替換公理。...
結合公理(axiom of incidence)是基本的幾何公理之一,亦稱關聯公理或從屬公理,是規定基本對象點、直線、平面之間從屬關係的一組公理,是希爾伯特公理系統中的第Ⅰ組...
調和公理數用於定義調和空間的基本公設。調和公理系統包含四個公理:正值性公理、可解性公理、完備性公理和收斂性公理。可解性公理可解集 編輯 ...
正則公理(也叫做基礎公理)是 Zermelo-Fraenkel 集合論的公理之一。...... 另外,不包含正則公理的康托的集合論,實際上假定了以自身為一個元素的集合的存在。...
和集公理,即並集公理,實際上說的是,給定集合A,我們可以找到一個集合B,它的元素完全是A的元素的元素。根據外延公理這個集合B是唯一的,它叫做A(中元素)的並集,...
從已知的一些函式依賴,可以推導出另外一些函式依賴,這就需要一系列推理規則,這些規則常被稱作“Armstrong 公理”。...
羅素公理體系--即有符合條件的書的確構成了一個集合,因為它們可以與其它的書進一步構成更大的整體(集合的定義)--比如它們和不符合條件的書共同構成了圖書館裡所有...
康托爾公理指的是在Zermelo-Fränkel集合論中,聲稱任何集合A的冪集(所有子集的集合)的勢嚴格大於A的勢。康托爾定理對於有限集合是明顯的,但是令人驚奇的是它...
形式公理主義(formalism)亦稱形式公理學派.數學基礎理論的分支之一其觀點如下:1.就“無窮觀”問題而言,認為古典數學中包含“絕對無窮”(實無限)概念的命題確實是“...
