策梅洛-弗蘭克爾集合論(Zermelo-Fraenkel Set Theory),含選擇公理時常簡寫為 ZFC,是在數學基礎中最常用形式的公理化集合論。不含選擇公理的則簡寫為ZF。
基本介紹
- 中文名:策梅洛-弗蘭克爾集合論
- 外文名:Zermelo-Fraenkel Set Theory
- 簡稱: ZFC
- 性質:公理化集合論
簡介
缺陷
公理
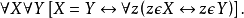
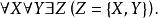
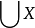


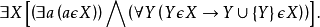
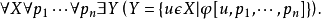

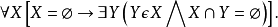

策梅洛-弗蘭克爾集合論(Zermelo-Fraenkel Set Theory),含選擇公理時常簡寫為 ZFC,是在數學基礎中最常用形式的公理化集合論。不含選擇公理的則簡寫為ZF。
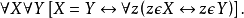
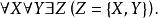
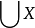


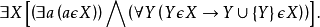
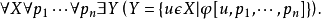

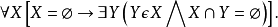
策梅洛-弗蘭克爾集合論(Zermelo-Fraenkel Set Theory),含選擇公理時常簡寫為 ZFC,是在數學基礎中最常用形式的公理化集合論。不含選擇公理的則簡寫為ZF。...
3)ZFC:策梅洛-弗蘭克爾集合論,包括選擇公理。選擇公理舉例說明 編輯 為令讀者有進一步的了解,以下是一些例子:選擇公理數學化例子 1a. 如果C為{1,2,3,…}的...
同倫類型論(homotopy type theory,縮寫HoTT)是一套旨在於同倫論的大框架下構建...1908年,恩斯特·策梅洛提出了被稱作策梅洛-弗蘭克爾集合論(或ZFC)的公理化...
最後一步,構造 S成為一個無限並集,需要代換公理;這條公理在1922年被加入策梅洛集合論,成為如今通用的策梅洛-弗蘭克爾集合論。 所以,儘管一般數學可以在 SN中進行...
尼爾森用完全公理化的方式構建了非標準分析;他稱之為內含集合論(Internal Set Theory)或IST,IST是策梅洛-弗蘭克爾集合論(含選擇公理,即ZFC)的延伸。其中除了元素...
許多常見的公理系統,如一階皮亞諾公理和包含策梅洛-弗蘭克爾集合論的公理化集合論等,都可以形式化成一階理論。然而,一階定理並沒有能力去完整描述及範疇性地建構...
儘管曾具有爭議性,選擇公理現在已被大多數數學家毫無保留地使用著,例如帶有選擇公理的策梅洛-弗蘭克爾集合論(ZFC)。數學家們使用選擇公理的原因是,有許多被普遍接受...
完全性定理等價於超濾子引理,它是弱形式的選擇公理,在不帶有選擇公理的策梅洛-弗蘭克爾集合論中有著等價的可證明性。完全性定理證明 編輯 哥德爾對定理的原始證明...
例如,透過二階算術可定義一階算術基於N為真;而透過一階策梅洛-弗蘭克爾集合論(ZFC)可定義二階算術(直到n階算術)的真式子。 雷蒙·史慕揚(Raymond Smullyan)強烈...
策梅洛-弗蘭克爾集合論中的正則公理,就是斷言所有的集合都是良基的。 [1] 無窮降鏈升鏈條件 編輯 數學上,偏序集P適合升鏈條件,若任意P的元素的升鏈a1≤a2...
《存在與事件》的出版正式宣告了一 個數學本體論的巴迪歐的出世。他充分吸納了康托爾的集合論,尤其是策梅洛-弗蘭克爾公理化定理、哥德爾的集合結構理論、科恩的力...
,所以,從並集公理可以得出包含公理:對任意兩集 X 與 Y,存在同時以 X,Y 為子集的集合。[1] 包含公理策梅洛-弗蘭克爾集合論 編輯 策梅洛-弗蘭克爾集合論的公...
在集合論中,一個集合x稱為是一個良基集合,如果集成員關係在x的傳遞閉包上是良基的。策梅洛-弗蘭克爾集合論中的正則公理,就是斷言所有的集合都是良基的。...
